Silva Fennica

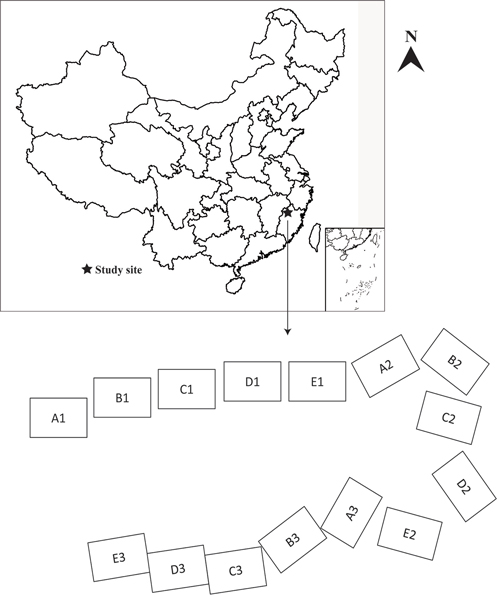
Fig. 1. Plot distributions and location of Chinese fir plantations used for modelling height-diameter allometry.

Table 1. Statistics of stand-and tree-level variables used for modelling height-diameter allometry of Chinese fir in this study.
Planting Density (PD)	BA (m² ha^–1)		N (tree/ha)		HD (m)		DBH (cm)		H (m)
Planting Density (PD)	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
A (1667 trees/ha)	33.03	19.84	1588.27	193.43	14.60	6.69	15.61	7.32	12.20	6.24
B (3333 trees/ha)	36.99	20.63	3094.15	513.69	13.14	6.12	12.59	5.86	10.94	5.51
C (5000 trees/ha)	40.47	21.95	4415.94	976.48	13.61	6.45	12.04	5.87	11.22	5.74
D (6667 trees/ha)	44.58	24.36	5705.04	1412.55	12.77	6.28	11.21	5.36	10.66	5.34
E (10 000 trees/ha)	42.21	19.97	7719.66	2794.09	12.27	5.94	9.87	5.13	9.41	4.87
BA: Stand basal area, N: Number of trees per ha; HD: stand dominant height; DBH: diameter at breast height; H: Tree height. Mean and SD calculated over the 17 instances of field sampling measurements taken from 1984–2010 (with each sampling instance occurring every year from 1984 to 1990, and every other year from 1992 to 2010).

Table 2. Summary statistics of climate variables for the years 1984–2010 used for modelling height-diameter allometry. Values in parentheses are minimum and maximum values.
Climate variable	Description	Mean
MAT (°C)	Mean annual temperature	18.96 (18.10, 19.80)
MWMT (°C)	Mean warmest month temperature	28.26 (26.50, 30.30)
MCMT (°C)	Mean coldest month temperature	8.34 (5.20, 10.20)
AP (mm)	Annual precipitation	1795.79 (1390.00, 2416.00)
AHM	Annual heat-moisture index	16.45 (11.90, 21.40)
SMMT (°C)	Summer mean maximum temperature	32.10 (30.30, 33.80)
WMMT (°C)	Winter mean minimum temperature	4.95 (2.50, 6.60)
SMT (°C)	Spring (Mar.–May) mean temperature	18.53 (16.90, 19.60)

Table 3. Inference rules for determining if variables have an effect on tree height using the Bayesian model averaging (BMA) posterior probability.
Probability	Effect of x_j on tree height
P(β_j ≠ 0 \| y) < 0.5	no effect
0.5 ≤ P(β_j ≠ 0 \| y) < 0.75	weak effect
0.75 ≤ P(β_j ≠ 0 \| y) < 0.95	positive effect
P(β_j ≠ 0 \| y) ≥ 0.95	strong effect

Table 4. The top five models selected and their posterior probabilities (post prob) of tree height-diameter allometry through Bayesian model averaging (BMA) and the model selected by stepwise approach (SR). The BMA model that has same variables as the SR model is in bold.
BMA models			SR Model
Models	Post prob		DBH, PD, HD, BA, MAT, MCMT, SMMT, WMMT
Model 1	(0.454)	DBH, PD, HD, BA, MAT, MCMT, SMMT
Model 2	(0.312)	DBH, PD, HD, BA, MAT, SMMT, WMMT
Model 3	(0.127)	DBH, PD, HD, BA, MAT, MCMT, SMMT, WMMT
Model 4	(0.082)	DBH, PD, HD, BA, MAT, MCMT, AHM, SMMT
Model 5	(0.016)	DBH, PD, HD, BA, MCMT, SMMT
BA: Stand basal area, HD: stand dominant height; DBH: diameter at breast height; H: Tree height; PD: planting density; MAT: mean annual temperature; MCMT: mean coldest month temperature; SMMT: Summer mean maximum temperature; WMMT: Winter mean minimum temperature; AHM: Annual heat-moisture index.

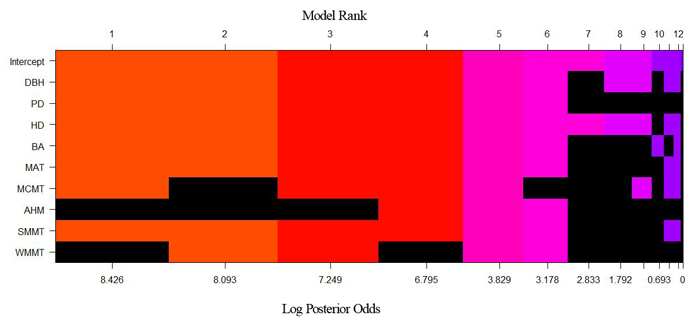
Fig. 2. Height-diameter model space through Bayesian model averaging (BMA). Each column represents one of the candidate models. The variables in black and other colors for each column are excluded and included in a model, respectively. The different colors of each column included in a model were used to help visually contrast differences in model ranking. The width of the column is proportional to the model’s posterior probability on the axis. View larger in new window/tab.

Table 5. Evaluation statistics of model prediction determined by Bayesian model averaging (BMA) and stepwise (SR) methods for modelling height-diameter allometry.
Statistics	BMA	SR
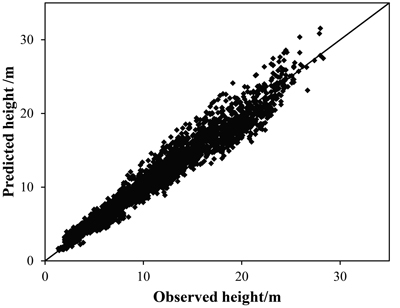
R²	0.9541	0.9540
MD	0.0018	–0.0078
MAD	0.9042	0.9043
MD: mean difference; MAD: mean absolute difference.

Fig. 3. Relationship between predicted height from Bayesian model averaging (BMA) and observed height based on the validation dataset.

Table 6. The parameter estimates determined by Bayesian model averaging (BMA) and stepwise (SR) methods for modelling height-diameter allometry.
Variable	SR			BMA
Variable	Mean	95%CI	P-value	Mean	95% CI	PP
Intercept	0.599	–0.177, 1.574	>0.05	2.263	2.260, 2.266	1.000
DBH	0.540	0.526, 0.664	<0.01	0.540	0.527, 0.554	1.000
PD	0.106	0.099, 0.114	<0.01	0.106	0.099, 0.113	0.999
HD	0.678	0.664, 0.695	<0.01	0.678	0.661, 0.690	0.999
BA	–0.099	–0.107, –0.091	<0.01	–0.099	–0.107, –0.089	1.000
MAT	0.563	0.341, 0.784	<0.01	0.498	0.241, 0.648	0.991
MCMT	–0.059	–0.099, –0.018	<0.01	–0.056	–0.123, –0.055	0.714
AHM	-	-	>0.05	0.002	0.000, 0.032	0.098
SMMT	–0.989	–1.250, –0.728	<0.01	–0.974	–1.275, –0.670	1.000
WMMT	–0.037	–0.064, –0.010	<0.01	–0.024	–0.070, 0.000	0.413
BA: Stand basal area, HD: stand dominant height; DBH: diameter at breast height; PD: planting density; MAT: mean annual temperature; MCMT: mean coldest month temperature; SMMT: Summer mean maximum temperature; WMMT: Winter mean minimum temperature; AHM: Annual heat-moisture index; CI: confidence interval for SR, and credible interval for BMA. PP: Posterior probability from BMA and values in bold indicate that variables have a strong effect on tree height.

Table 7. Summary of the scale of height-diameter allometry.
Scale	Study by Mcmahon and Kronauer (1976)			Study by Zhang et al. (2019)	This study
	Stress similarity	Elastic similarity	Geometric similarity
	0.50	0.66	1.00	Close to 0.5	0.54