Using a bivariate generalized linear mixed model to analyze the effect of feeding pressure on pine weevil damage
Lappi J., Luoranen J. (2016). Using a bivariate generalized linear mixed model to analyze the effect of feeding pressure on pine weevil damage. Silva Fennica vol. 50 no. 1 article id 1496. https://doi.org/10.14214/sf.1496
Highlights
- Probability of damage of treated seedlings can be predicted from the probability of damage of control seedlings (feeding pressure).
Abstract
The objective of the study is to derive a method by which one can analyze how the probability of damage made by pine weevils on seedlings treated with insecticides depends on the probability of damage on untreated control seedlings, called feeding pressure. Because the probabilities vary from stand to stand and from block to block, the analysis is done using a generalized linear mixed model. The dependency of probability of damage on the feeding pressure cannot be properly analyzed using observed relative frequency of damage of control seedlings as a covariate, but it can be analyzed using a bivariate model. One equation describes damage of control seedlings and another equation damage of treated seedlings. The random stand and block effects of different equations are correlated. For a given probability of stand level control seedling damage, the random stand effect for control seedlings can be computed using a link function, then random stand effects for treated seedlings can be predicted using the best linear predictor from the random effect for control seedlings. Using an inverse link the prediction can again be presented in the probability scale which is of interest to the user. Using these three steps the probability of damage of treated seedlings can be predicted from the control damage probability. The probability of damage of treated seedlings can also be predicted from the observed relative frequency of damaged control seedlings using simulation. The complementary log-log link was used for control seedlings and the log-log link for treated seedlings.
Keywords
measurement error;
best linear predictor;
correlated random effects;
log-log link
-
Lappi,
Natural Resources Institute Finland (Luke), Economics and society, Juntintie 154, FI-77600 Suonenjoki, Finland
E-mail
juha.lappi@luke.fi

- Luoranen, Natural Resources Institute Finland (Luke), Management and Production of Renewable Resources, Juntintie 154, FI-77600 Suonenjoki, Finland E-mail jaana.luoranen@luke.fi
Received 14 September 2015 Accepted 28 December 2015 Published 4 January 2016
Views 35765
Available at https://doi.org/10.14214/sf.1496 | Download PDF

1 Introduction
The pine weevil (Hylobius abietis) inflicts considerable damage on conifer regeneration areas in a large part of Europe. There have been several studies on pine weevil ecology and modeling of how pine weevil damage depends on stand properties and different chemical and soil preparation methods (e.g. Örlander and Nilsson 1999; Nordlander et al. 2005, 2011). However, these papers have not related damage under different treatments in the same regeneration areas; the analysis has been concentrated on how different treatments differ marginally. In this paper we develop a method for comparing different treatments in the same stand.
In our data each stand has several blocks. In each block in each stand there is a plot, called the control, on unprepared soil, and another plot on mounded soil planted with seedlings treated with an insecticide. For the current analysis the probability of damage of seedlings on unprepared soil in the stand indicates the amount of weevils in the neighborhood, and is called feeding pressure. The feeding pressure is a theoretical latent variable. Feeding pressure can be measured with observed relative frequencies of damaged seedlings on unprepared plots, but as the observed relative frequencies vary around the true probabilities, these measurements contain random measurement error.
The feeding pressure can also be explained by some other factors, but for this study the amount of weevils in the neighborhood results only from its own upper level stochastic process, and we would like to make inference conditional on it. Decision whether to make treatment or not can be made knowing the distribution of feeding pressure and the probability of damage of treated seedlings for each level of feeding pressure. The dependent variable in our analysis is the binary variable indicating whether a seedling is damaged or not. The probabilities evidently vary randomly between stands and possibly between blocks within stands, thus a generalized linear mixed model (GLMM, see Stroup 2013 and Demidenko 2004) is a natural methodological framework for analyzing our data.
We thus want to model how the damages on treated plots depend on the feeding pressure. For two reasons this cannot be properly modeled by using the measured feeding pressure, i.e., the observed relative frequency of damage of control seedlings, as an explanatory variable in a GLMM. First, using measured feeding pressure as an explanatory variable in a GLMM would lead to a model where the probability of damage of treated seedlings does not go to zero when the feeding pressure goes to zero. This would be illogical. Secondly, it is well known that measurement errors of the independent variables lead biased estimates in statistical modeling. The first obstacle could be circumvented by using logarithm or inverse of the measured feeding pressure (augmented by a small constant) as a covariate, but the second obstacle would require complicated modeling (e.g. Torabi 2013).
The effect of feeding pressure can be solved nicely using a bivariate GLMM with correlated random effects. One equation describes the damage on the control plots and second correlated equation describes the damage on treated plots. It is then possible to derive how the probability of damage on treated plots depends on the probability of damage on control plots (feeding pressure).
To concentrate on the feeding pressure, we do not include in the model all the predictors available in the data. We use just one seedling level predictor, distance to the humus, as an example. We used the SAS GLIMMIX procedure for the analysis (SAS for Windows, SAS 9.3 TS Level 1M2x64_7PRO platform; SAS institute Inc., Cary, NC, USA). As there was a seedling level predictor in the model, we had to analyze the data as binary data (not as binomial data). The Laplace method was used in the analysis as there were convergence problems when using Gaussian quadrature which would otherwise be preferred (Stroup 2013). Logit, probit, log-log, and complementary log-log links will all be considered.
2 Data
In spring 2012 and spring 2013, Norway spruce (Picea abies [L.] Karst.) container seedlings were planted on 11 and 9 regeneration areas (stands), respectively, in central Finland. Regeneration areas were mounded before planting. Before planting, a part of the seedlings were treated with an insecticide (lambda-cyhaltorin 100 g L–1, KarateZeon-tekniikka). In each stand, seedlings were planted in four blocks. In each block, 25 treated seedlings were planted onto the mounds, one seedling per mound. In addition, 25 (10 in 2012) seedlings were also planted between the mounds onto the unprepared soil (control). Feeding of pine weevils on seedlings was checked in the autumn of the planting year. Feeding was coded as 0if no feeding scars were found and 1 if there was even a small scar on the stem of a seedling. At planting, seedling distance to the nearest humus was also measured to an accuracy of 1 cm. Fig. 1 shows the dependency of relative stand frequencies of damage of treated and control seedlings.
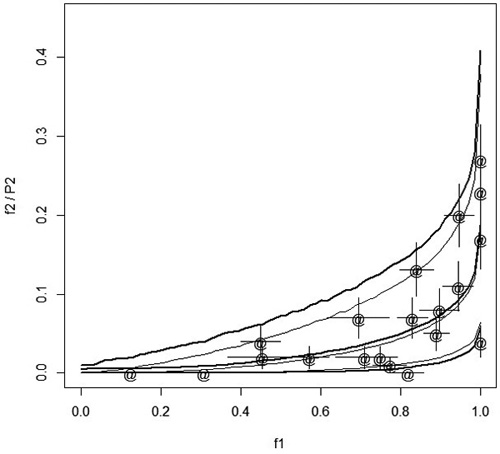
Fig. 1. Points (marked with ‘@’) show he relative frequencies of damaged treated seedlings, f2, in different stands with respect to the relative frequency of damaged control seedlings, f1. The error bars in both directions indicate the standard error computed as ![]() . The thin solid lines describe the median and 95% confidence interval when the probability of damage of treated seedlings, P2i, is predicted from f1 using the estimated model and simulation assuming that each stand has four plots with 17 seedlings in each plot. The thick solid lines show the median and 95% confidence interval when f2 is predicted from f1.
. The thin solid lines describe the median and 95% confidence interval when the probability of damage of treated seedlings, P2i, is predicted from f1 using the estimated model and simulation assuming that each stand has four plots with 17 seedlings in each plot. The thick solid lines show the median and 95% confidence interval when f2 is predicted from f1.
3 Method and results
The model for the control plots was:
where ![]() is the indicator variable for damage of seedling k in the control plot in block j in stand i, μ1 is a fixed constant, and
is the indicator variable for damage of seedling k in the control plot in block j in stand i, μ1 is a fixed constant, and ![]() and
and ![]() are random stand and block (or plot) effects, respectively. We have no way to separate block and plot effects using our data. For separate models it would be better to describe these effects as plot effects, but when considering the models simultaneously, these effects need to be described as block effects. Thus we use the block effect term throughout.
are random stand and block (or plot) effects, respectively. We have no way to separate block and plot effects using our data. For separate models it would be better to describe these effects as plot effects, but when considering the models simultaneously, these effects need to be described as block effects. Thus we use the block effect term throughout.
For treated plots we have the model:
where α0 and α1 are fixed parameters, xijk is the distance to the humus, and ![]() and
and ![]() are random stand and block effects, respectively.
are random stand and block effects, respectively.
We assume that the random stand and block effects are correlated across equations, and the joint distribution of random effects is multivariate normal. The obtained model is a multivariate model at stand and block level but not at seedling level as y1 and y2 cannot be measured from the same seedling. Let us denote that ![]() and
and ![]() . These covariances can be estimated by putting the data for different models together and using dummy variables to select the appropriate components for each observation. GLIMMIX also allows to specify different link functions to different equations (observations). The complete model (which can be utilized when writing the SAS code) can be written:
. These covariances can be estimated by putting the data for different models together and using dummy variables to select the appropriate components for each observation. GLIMMIX also allows to specify different link functions to different equations (observations). The complete model (which can be utilized when writing the SAS code) can be written:
where t = 1 for control seedlings and t = 2 for treated seedlings, h1ijk and h2ijk are the indicator variables for the control and treated seedlings, respectively, x2ijk is distance to humus for treated seedlings.
We are interested in how the probability of damage to treated seedlings depends on the probability of damage to seedlings in unprepared soil. These stand level probabilities are defined as the probabilities of damage if the random plot effects are zero and the distance to humus is equal to the mean of the whole data. The stand averages of the distance to humus are very close to the overall average, thus doing the analysis also with respect different values of stand averages ![]() would not be informative (and
would not be informative (and ![]() is not generally known). Let us denote these stand damage probabilities as Pti , i.e.
is not generally known). Let us denote these stand damage probabilities as Pti , i.e.
where link –1 is the inverse link function for control seedlings (link1) and for treated seedlings (link2), and ![]() is the overall average of distance to humus. P1i is our theoretical measure for feeding pressure. Because of the nonlinearity of the link functions these stand probabilities are not the averages of plot probabilities. Let us then look at how the damage to seedlings on treated plots depends on the feeding pressure. We are interested in predicting (explaining) P2i with P1i even if in practice P1i is never known (but its distribution is implied by Eqs. 1 and 2). If P1i is given, then we can solve a1i from Eq. 7, i.e.
is the overall average of distance to humus. P1i is our theoretical measure for feeding pressure. Because of the nonlinearity of the link functions these stand probabilities are not the averages of plot probabilities. Let us then look at how the damage to seedlings on treated plots depends on the feeding pressure. We are interested in predicting (explaining) P2i with P1i even if in practice P1i is never known (but its distribution is implied by Eqs. 1 and 2). If P1i is given, then we can solve a1i from Eq. 7, i.e.
![]()
When a1i is known then the conditional expectation of a2i, which is thus the best predictor (see McCulloch and Searle 2001), is:

and the variance of the prediction error is

Then using Eq. 10 in Eq. 8 we get:
Adding ![]() to
to ![]() we get a 95% confidence interval for the predicted
we get a 95% confidence interval for the predicted ![]() . Note that when P1i approaches 1,
. Note that when P1i approaches 1, ![]() also approaches 1, which seems to be in contradiction with Fig. 1. Note that in Eq. 12 we can also use the distance to humus of an individual seedling instead the average distance.
also approaches 1, which seems to be in contradiction with Fig. 1. Note that in Eq. 12 we can also use the distance to humus of an individual seedling instead the average distance.
We tried logit, probit, log-log (ll) and complementary log-log (cll) links. The best –2 log likelihood and Pearson’s chi-square fit was obtained when the cll-link was used for control seedlings and the ll-link for treated seedlings. The relative frequencies of the damage of control seedlings and treated seedlings are close to one or zero, respectively. In such cases the complementary log-log link is useful according to Stroup (2013, p. 317). Evidently also the log-log link should be considered in such cases.
The log-log link is
which has the inverse link for a linear predictor η
The complementary log-log link is
with the inverse link
The model obtained by using the log-log link and coding damage as 1 is equivalent to the model where no damage is coded as 1 and a complementary log-log link is used (and vice versa). Note that ll- and cll-links are nonsymmetrical unlike probit and logit links, thus coding ‘success’ differently leads to a different model.
The parameter estimates obtained were:
![]() and
and ![]() (the correlation between a1i and a2i was thus 0.93). For block effects
(the correlation between a1i and a2i was thus 0.93). For block effects ![]() and
and ![]() (the correlation between b1ij and b2ij was thus 0.33). The variances and the covariance of block effects were much lower than the variances and the covariance of the stand effects, and only the between block variance of the control seedlings was significant. The variances of random effects of control seedlings are much larger than variances of treated seedling. This shows that such a univariate GLMM where same random effects would apply for both control and treated seedlings would not be a reasonable alternative for the proposed bivariate GLMM. Fig. 2 shows predicted P2i and the 95% confidence intervals.
(the correlation between b1ij and b2ij was thus 0.33). The variances and the covariance of block effects were much lower than the variances and the covariance of the stand effects, and only the between block variance of the control seedlings was significant. The variances of random effects of control seedlings are much larger than variances of treated seedling. This shows that such a univariate GLMM where same random effects would apply for both control and treated seedlings would not be a reasonable alternative for the proposed bivariate GLMM. Fig. 2 shows predicted P2i and the 95% confidence intervals.
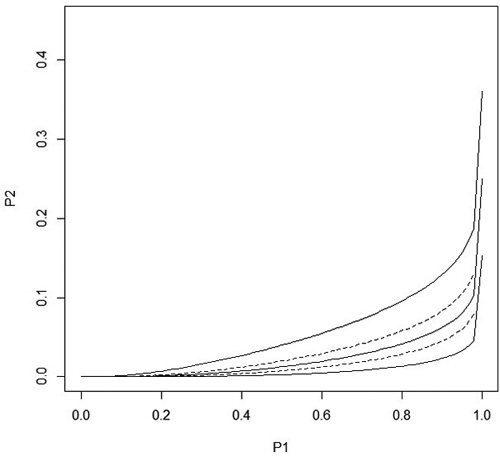
Fig. 2. The solid lines show the predicted stand level probability of damage ![]() and the 95% confidence interval in treated seedlings as a function of the stand level probability P1i of damage in control seedlings when distance to the humus is equal to its overall average. The maximum value for P1i is P1i = 0.9999995 which is the upper 95% confidence limit for P1i. The dashed lines are obtained when the distance to the humus is the average value ± sd. All curves go to one when P1i goes to one.
and the 95% confidence interval in treated seedlings as a function of the stand level probability P1i of damage in control seedlings when distance to the humus is equal to its overall average. The maximum value for P1i is P1i = 0.9999995 which is the upper 95% confidence limit for P1i. The dashed lines are obtained when the distance to the humus is the average value ± sd. All curves go to one when P1i goes to one.
One condition for the model to be logical is that the stand probability of damage of treated seedlings, P2i , is clearly less than the probability of damage of control seedlings, P1i , in all stands, not just on average. This is clearly the case in the range of P1i values shown in Fig. 2, even if P2i approaches P1i when P1i approaches one.
Up to now we have considered the prediction of P2i with P1i . In principle, it could be of interest to predict P2i using observed relative frequency of damage of control seedlings (‘measured feeding pressure’). In our special case, this is not of interest as it would take too long to test the control seedlings before planting the whole stand, but in other applications of the method this may be of interest. With our model, the prediction of P2i from the observed relative frequency of damaged control seedlings is easy using simulation. As an example, we simulated one million stands with four blocks. Each block had a control plot having 17 seedlings. This correspond roughly the average situation in our data where we had 10 or 25 seedlings in the control plots. The distance to the humus was equal to the overall average. Classifying the data with respect to the observed relative frequency of damaged control seedlings we computed the median and 95% confidence interval of P2i for each relative frequency. The result is shown in Fig.1 with thin solid lines. Comparing Fig. 1 to Fig. 2 we note that the confidence interval is wider when P2i is predicted from the relative frequency than from true (unknown) P1i. When the relative frequency of control seedling damage is exactly 1, the upper confidence limit is 0.38. In contrary, when P1i is one, then both the lower and upper confidence limit of P2i is also one.
Also the relative frequency of the damage of treated seedlings, f2, was simulated according to the estimated model. The number of treated seedlings in a block was 25, as in our data. The thick lines in Fig.1 show the median and confidence interval for f2. The confidence interval shows that the observed relative frequencies fall reasonably well within the confidence interval. When f1 was 1, then the upper confidence limit for f2 was 0.41, which is in agreement with the data and which demonstrates that the exact behavior of P2i when P1i goes to one cannot be inferred from relative frequencies in a moderately small data set. As the distance to humus was assumed to be constant, the simulation could be done plot wise using binomial distribution. The simulation took a couple of seconds.
4 Discussion
We have demonstrated that the problem of predicting one probability from another probability can be made in a simple way using a bivariate generalized linear model with correlated random effects. Intuitively the other probability is a covariate, but trying to put the probability into the model directly using observed relative frequency leads to theoretical and practical problems, as discussed in the introduction. We hope that the approach presented can also be applied in other settings.
A problem in the data analysis was that we were forced to use Laplace method in the estimation of the GLMM instead of Gaussian quadrature. A probable reason for the convergence problems was that our data set is rather small and the random stand effects were highly correlated. However, obtaining better estimates for the parameters would not change our methodology, which is the main focus in this paper.
We applied the ll-link to treated seedlings and cll-link to control seedlings. In the literature (e.g. by Stroup 2013) usually only a cll-link is presented. We think that if there is no theoretical reason for preferring a cll-link (as Fisher 1922 had in when estimating the density of infective organisms), both should be considered. A model with an ll-link can be obtained by changing the coding of success and continuing to use a cll-link, but it is more straightforward to work directly with the ll-link.
Here we had two simultaneous equations. In our data we also have a third dimension, the damage of seedlings in mounded plots without chemical treatment. The level of damage of seedlings in mounded plots without treatment is between that of the control and treated plots. This third dimension is important with respect to silvicultural decision making, but methodologically it does not require any new concepts, so it will be analyzed later.
It would be interesting to obtain a theoretical explanation for the obtained link functions. Some explanation could be obtained for the cll-link by assuming a compound Poisson process for the pine weevil density and a constant risk zone around a seedling, but the obtained estimate for weevil density was not compatible with the estimate obtained using untreated seedlings planted on mounded plots. No explanation could be reached for the damage of treated seedlings, i.e., when the ll-link was used. In any case, the ecology of the pine weevil is quite complicated and no simple explanation could be anticipated.
It is an open question, should the predicted probability for treated seedlings, P2i , go to one when P1i goes to one, as it does in our model. The simulation result that the confidence interval was below 0.41 when the observed relative frequency was one shows that relative frequencies in Fig. 1 cannot be used as evidence that P2i should not approach one. It would require a large data set with many plots in a stand to see what really happens at high P1i . Formulating the model so that P2i does not go to one when P1i goes to one cannot be done in a simple way in the GLMM framework.
The feeding pressure can be explained with some stand level variables. Thus, if these variables are used in the model for treated seedlings they will also be significant predictors. It is of interest to test if these variables operate only via feeding pressure, or if they also have an additional direct effect. This can be tested by testing if these variables are significant after putting the linear predictor of feeding pressure into the model (of course one predictor needs to be dropped in order to avoid linear dependencies between the predictors).
Using our model we can both predict P2i from P1i and estimate the distribution of P1i . Thus based on our model, the decision maker can start to use also quantitative decision making methods (see e.g. Kangas et al. 2015) when deciding whether to make the treatment or not. For instance, after determining the utility of forest regeneration result for different damage proportions, the decision maker can maximize the expected utility. The presented model for the distribution of P1i is very rough. It will be developed further in the future by adding stand variables to the model.
References
Demidenko E. (2004). Mixed models. John Wiley & Sons, Hoboken, New Jersey. http://dx.doi.org/10.1002/0471728438.
Fisher R.A. (1922). On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society 222: 309–368. http://dx.doi.org/10.1098/rsta.1922.0009.
Kangas A., Kurttila M., Hujala T., Eyvindson K., Kangas J. (2015). Decision support for forest management. Second edition. Managing Forest Ecosystems 30, Springer. http://dx.doi.org/10.1007/978-3-319-23522-6.
McCulloch C.E., Searle S.R. (2001). Generalized, linear and mixed models. John Wiley & Sons, New York.
Nordlander G., Nylund H., Björklund N. (2005). Soil type and microtopography influencing feeding above and below ground by the pine weevil Hylobius abietis. Agricultural and Forest Entomology 7: 107–113. http://dx.doi.org/10.1111/j.1461-9555.2005.00257.x.
Nordlander G., Hellqvist C., Johansson K., Nordenhem H. (2011). Regeneration of European boreal forests: effectiveness of measures against seedling mortality caused by the pine weevil Hylobius abietis. Forest Ecology and Management 262: 2354–2363. http://dx.doi.org/10.1016/j.foreco.2011.08.033.
Örlander G., Nilsson U. (1999). Effect of reforestation methods on pine weewil (Hylobius abietis) damage and seedling survival. Scandinavian Journal of Forest Research 14: 341–354. http://dx.doi.org/10.1080/02827589950152665.
Stroup W.W. (2013). Generalized linear mixed models. CRC Press, Boca Raton, Florida. 555 p. ISBN 9781439815120.
Torabi M. (2013). Likelihood inference in generalized linear mixed measurement error models. Computational Statistics & Data Analysis 57(1): 549–557. http://dx.doi.org/10.1016/j.csda.2012.07.018.
Total of 9 references.
Send to email

