Large-scale two-phase estimation of wood production by poplar plantations exploiting Sentinel-2 data as auxiliary information
Marcelli A., Mattioli W., Puletti N., Chianucci F., Gianelle D., Grotti M., Chirici G., D' Amico G., Francini S., Travaglini D., Fattorini L., Corona P. (2020). Large-scale two-phase estimation of wood production by poplar plantations exploiting Sentinel-2 data as auxiliary information. Silva Fennica vol. 54 no. 2 article id 10247. https://doi.org/10.14214/sf.10247
Highlights
- A two-phase sampling for large-scale assessment of fast-growing forest crops is developed
- Vegetation indices from Sentinel-2 are exploited in a linear regression estimator
- The linear regression estimator turns out to be better than the estimator based on the sole sample information
- The approach represents a reference for supporting outside-forest resource monitoring and assessment.
Abstract
Growing demand for wood products, combined with efforts to conserve natural forests, have supported a steady increase in the global extent of planted forests. Here, a two-phase sampling strategy for large-scale assessment of the total area and the total wood volume of fast-growing forest tree crops within agricultural land is presented. The first phase is performed using tessellation stratified sampling on high-resolution remotely sensed imagery and is sufficient for estimating the total area of plantations by means of a Monte Carlo integration estimator. The second phase is performed using stratified sampling of the plantations selected in the first phase and is aimed at estimating total wood volume by means of an approximation of the first-phase Horvitz-Thompson estimator. Vegetation indices from Sentinel-2 are exploited as freely available auxiliary information in a linear regression estimator to improve the design-based precision of the estimator based on the sole sample data. Estimators of the totals and of the design-based variances of total estimators are presented. A simulation study is developed in order to check the design-based performance of the two alternative estimators under several artificial distributions supposed for poplar plantations (random, clustered, spatially trended). An application in Northern Italy is also reported. The regression estimator turns out to be invariably better than that based on the sole sample information. Possible integrations of the proposed sampling scheme with conventional national forest inventories adopting tessellation stratified sampling in the first phase are discussed.
Keywords
national forest inventories;
Sentinel-2;
design-based inference;
first-phase tessellation stratified sampling;
regression estimator;
second-phase stratified sampling;
simulation study
-
Marcelli,
University of Tuscia, Department for Innovation in Biological, Agro-food and Forest systems, Viterbo, Italy; Fondazione Edmund Mach, Department of Sustainable Agro-Ecosystems and Bioresources, Research and Innovation Centre, San Michele all’Adige, Italy
E-mail
agnese.marcelli@student.unisi.it

- Mattioli, University of Tuscia, Department for Innovation in Biological, Agro-food and Forest systems, Viterbo, Italy; CREA, Research Centre for Forestry and Wood, Arezzo, Italy E-mail walter.mattioli@crea.gov.it
- Puletti, CREA, Research Centre for Forestry and Wood, Arezzo, Italy E-mail nicola.puletti@crea.gov.it
- Chianucci, CREA, Research Centre for Forestry and Wood, Arezzo, Italy E-mail fchianucci@gmail.com
- Gianelle, Fondazione Edmund Mach, Department of Sustainable Agro-Ecosystems and Bioresources, Research and Innovation Centre, San Michele all’Adige, Italy E-mail damiano.gianelle@fmach.it
- Grotti, CREA, Research Centre for Forestry and Wood, Arezzo, Italy; University of Roma La Sapienza, Department of Architecture and Design, Rome, Italy E-mail mirkogrotti@gmail.com
- Chirici, University of Firenze, Department of Agriculture, Food, Environment and Forestry, Florence, Italy E-mail gherardo.chirici@unifi.it
- D' Amico, University of Firenze, Department of Agriculture, Food, Environment and Forestry, Florence, Italy E-mail giovanni.damico@unifi.it
- Francini, University of Firenze, Department of Agriculture, Food, Environment and Forestry, Florence, Italy; University of Molise, Department of Agricultural, Environmental and Food Sciences, Campobasso, Italy E-mail saverio.francini@gmail.com
- Travaglini, University of Firenze, Department of Agriculture, Food, Environment and Forestry, Florence, Italy E-mail davide.travaglini@unifi.it
- Fattorini, University of Siena, Department of Economics and Statistics, Siena, Italy E-mail lorenzo.fattorini@unisi.it
- Corona, CREA, Research Centre for Forestry and Wood, Arezzo, Italy E-mail piermaria.corona@crea.gov.it
Received 15 September 2019 Accepted 17 February 2020 Published 20 March 2020
Views 56597
Available at https://doi.org/10.14214/sf.10247 | Download PDF

1 Introduction
Growing demand for wood products, combined with efforts to conserve natural forests, have supported a 65% increase in the global extent of planted trees since 1990 (FAO 2015). Tree plantations contributed approximately to half the industrial roundwood production in 2012 (Payn et al. 2015). As distinctively concerns fast-growing tree plantations within agricultural farms, characterized by relatively short rotations and an intrinsic high dynamism in relation to the temporal variability of farmland destinations for cultivation, there is the need for a frequent updating of accurate and spatially detailed statistical data about tree species composition, stand structure and wood supply attributes. Such needs may exceed the scope of conventional forest inventories, making room for ad-hoc information sources (Alam et al. 2014).
From a methodological perspective, we have approached the large-scale estimation of fast-growing tree plantations by a two-phase probabilistic sampling scheme. Stratified or systematic schemes are usually adopted in the first phase of forest surveys to ensure a uniform sampling coverage over the survey area. Under this scenario, we have followed the proposal by Baffetta et al. (2011), adopting the tessellation stratified sampling (TSS) to select plantations in the first phase. TSS is based on covering the area by means of regular polygons of equal size, each of them containing at least a portion of the area, and then randomly selecting one point in each polygon. Plantations spotted by one or more sample points are selected. TSS choice is consistent with the trend of last years, in which TSS is becoming increasingly popular. Both Italian and U.S.D.A. Forest Services are currently adopting TSS in the first phase of their NFIs (Fattorini et al. 2006; Tomppo et al. 2010), while the Italian Ministry of Environment and Protection of Land and Sea adopts TSS in the first phase of the IUTI (from the Italian acronym of Inventario dell’Uso delle Terre d’Italia) land-use survey (Corona et al. 2012).
While the first phase – performed on screen using high-resolution remotely sensed imagery – is sufficient to estimate the total area of plantations by means of a Monte Carlo integration estimator, a second phase is necessary to reduce the sample size, achieving a stratified sampling of plantations to be visited on the ground. Once wood volumes are recorded for the plantations selected in the second phase, a two-phase estimator of total wood volume is derived starting from an approximation of the first-phase Horvitz-Thompson estimator, once again proposed by Baffetta et al. (2011) and suitable when units (in this case, fast-growing tree plantations within agricultural land, with size usually of few hectares) have extents much smaller than the survey area. Finally, the use of a linear regression estimator is proposed to exploit vegetation indices from high-resolution satellite images as auxiliary information, for improving the design-based precision of the estimator based on the sole sample information.
2 Material and methods
2.1 First-phase sampling and estimation
Denote by ![]() the population of N tree plantations in a delineated survey area
the population of N tree plantations in a delineated survey area ![]() of size
of size ![]() We superimposed a region of regular shape, say
We superimposed a region of regular shape, say ![]() of size
of size ![]() partitioned into R non-overlapping regular polygons
partitioned into R non-overlapping regular polygons ![]() of equal size (e.g. quadrats or hexagons) and such that
of equal size (e.g. quadrats or hexagons) and such that ![]() for all i = 1,...,R. We aimed at estimating the total area
for all i = 1,...,R. We aimed at estimating the total area ![]() of the region P constituted by the union of the N plantations, henceforth referred to as the coverage. We performed estimation as Monte Carlo integration, i.e. for each point
of the region P constituted by the union of the N plantations, henceforth referred to as the coverage. We performed estimation as Monte Carlo integration, i.e. for each point ![]() we considered the surface
we considered the surface
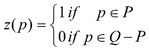
in such a way that the coverage to be estimated was expressed as the integral
![]()
Following the sampling scheme referred to as TSS (Stevens 1997; Barabesi and Franceschi 2011; Barabesi et al. 2012), we randomly located a point within each polygon and we recorded the surface value z at any sampled point exploiting satellite imagery or orthophotos. Then, we computed the standard Monte Carlo estimate of ![]() (e.g. Gregoire and Valentine 2008, chapter 4) by means of
(e.g. Gregoire and Valentine 2008, chapter 4) by means of
![]()
where R(P) was the number of sample points falling in P, and
![]()
was the fraction of sample points falling in P. We then estimated the design-based variance of (1) by means of

as if the R points were randomly and independently selected throughout the whole region ![]() Under TSS, the Monte Carlo estimator (1) is unbiased with variance that cannot be estimated unbiasedly, and the variance estimator (2) is conservative (Barabesi and Franceschi 2011; Barabesi et al. 2012). Finally, we computed a nominal 95% confidence interval by means of
Under TSS, the Monte Carlo estimator (1) is unbiased with variance that cannot be estimated unbiasedly, and the variance estimator (2) is conservative (Barabesi and Franceschi 2011; Barabesi et al. 2012). Finally, we computed a nominal 95% confidence interval by means of ![]()
We also aimed at estimating the total wood volume of plantations
![]()
where yj was the value of wood volume in the j-th plantation. Following Baffetta et al. (2011), we exploited TSS as a scheme for selecting plantations, in the sense that a plantation was selected when at least one of the R sample points falls inside it (Fig. 1).
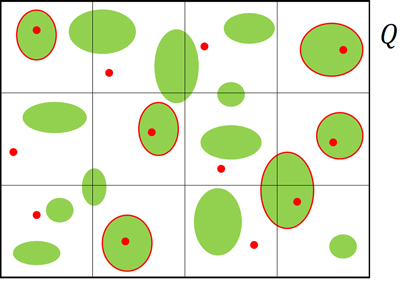
Fig. 1. Example of a population of tree plantations sampled by means of tessellation stratified sampling. The region Q is tessellated by 12 quadrats, the green ellipses represent plantations and the red points represent sample points. Plantations encircled in red are those selected in the first phase.
Therefore, if we were able to record the volume and the extent for each plantation in the set ![]() of the n poplar plantations selected by TSS, then we could use the following estimator of total wood volume
of the n poplar plantations selected by TSS, then we could use the following estimator of total wood volume

together with a conservative estimator of its design-based variance

where ![]() was the size of the j-th plantation. Baffetta et al. (2011) derived estimator (3) as an approximation of the familiar Horvitz-Thompson estimator, also providing the conservative estimator of its variance (4). The approximation was proposed because the direct use of the Horvitz-Thompson estimator would require the cumbersome quantification of the sizes of the portions of the selected plantations lying in adjacent polygons. The Authors proved that the approximation (3) is suitable when the sizes of patches to be sampled are small compared with the size of polygons, in such a way that patches are likely to lie within a unique polygon. Therefore, apart the pedagogical representation of Fig. 1, the considered fast-growing tree plantations within agricultural farms rarely straddle quadrat boundaries for quadrats sufficiently large.
was the size of the j-th plantation. Baffetta et al. (2011) derived estimator (3) as an approximation of the familiar Horvitz-Thompson estimator, also providing the conservative estimator of its variance (4). The approximation was proposed because the direct use of the Horvitz-Thompson estimator would require the cumbersome quantification of the sizes of the portions of the selected plantations lying in adjacent polygons. The Authors proved that the approximation (3) is suitable when the sizes of patches to be sampled are small compared with the size of polygons, in such a way that patches are likely to lie within a unique polygon. Therefore, apart the pedagogical representation of Fig. 1, the considered fast-growing tree plantations within agricultural farms rarely straddle quadrat boundaries for quadrats sufficiently large.
2.2 Second-phase sampling and estimation
The estimator of type (3) and its variance estimator (4) would require that each plantation selected in the first phase was visited on the ground, thus involving a prohibitive effort for ![]() large. To reduce sampling effort, we performed a second phase of sampling in which a sub-sample of plantations was selected from
large. To reduce sampling effort, we performed a second phase of sampling in which a sub-sample of plantations was selected from ![]() and subsequently visited.
and subsequently visited.
We selected the second-phase sample ![]() by means of stratified sampling. We partitioned the first-phase sample
by means of stratified sampling. We partitioned the first-phase sample ![]() into L strata
into L strata ![]() of size n1,...,nL and from each stratum we selected m1,...,mL plantations by means of simple random sampling without replacement (SRSWOR) (Fig. 2). Stratification can be performed on the basis of some criterion regarding plantation characteristics (e.g. tree species or clone, rotation age, etc.) or on the basis of spatial criteria. For example, strata can coincide with administrative districts in such a way that the uniform sampling coverage ensured in the first phase by TSS is maintained in the second phase. Regarding spatial stratification, it is worth noting that plantations lying in more than one spatial stratum must be assigned to one of them, in such a way to ensure a proper partition of the first-phase sample
of size n1,...,nL and from each stratum we selected m1,...,mL plantations by means of simple random sampling without replacement (SRSWOR) (Fig. 2). Stratification can be performed on the basis of some criterion regarding plantation characteristics (e.g. tree species or clone, rotation age, etc.) or on the basis of spatial criteria. For example, strata can coincide with administrative districts in such a way that the uniform sampling coverage ensured in the first phase by TSS is maintained in the second phase. Regarding spatial stratification, it is worth noting that plantations lying in more than one spatial stratum must be assigned to one of them, in such a way to ensure a proper partition of the first-phase sample ![]() without plantations belonging to more than one stratum.
without plantations belonging to more than one stratum.
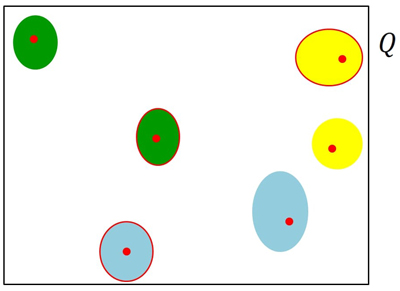
Fig. 2. Example of the stratified second-phase sampling. The six plantations selected in the first phase are partitioned into three strata (yellow, green and light blue plantations) and the 50% is selected from each stratum. Plantations encircled in red are those selected in the second phase.
Denoting by ![]() the set of plantations selected in the second phase in the stratum l, we estimated Ty by means of
the set of plantations selected in the second phase in the stratum l, we estimated Ty by means of

and we estimated its design-based sampling variance by means of
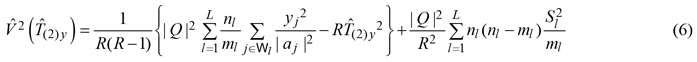
where
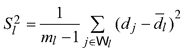
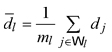
and ![]() It should be noticed that the double summand in equation (5) was the second-phase estimator of the summand in (3), based on the second-phase stratified sample
It should be noticed that the double summand in equation (5) was the second-phase estimator of the summand in (3), based on the second-phase stratified sample ![]() Moreover, the first term in (6) constitutes an unbiased estimator of the first-phase variance estimator (4), while the second term constitutes an unbiased estimator of the variance increase due to the second phase over the variance due to the first phase.
Moreover, the first term in (6) constitutes an unbiased estimator of the first-phase variance estimator (4), while the second term constitutes an unbiased estimator of the variance increase due to the second phase over the variance due to the first phase.
Finally, we computed a nominal 95% confidence interval by means of ![]()
2.3 Linear regression second-phase estimator
Denote by xj the value of a vegetation index derived from satellite imagery in the j-th plantation, available for each ![]() Assuming a linear relationship between the xj s and volume densities dj s, we exploited the auxiliary information provided by xj s adopting the second-phase simple regression estimator (Särndal et al. 1992, Chapter 6)
Assuming a linear relationship between the xj s and volume densities dj s, we exploited the auxiliary information provided by xj s adopting the second-phase simple regression estimator (Särndal et al. 1992, Chapter 6)

where
![]()
![]()
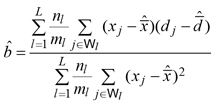
and
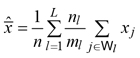
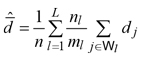
Practically speaking, while the summand in the first-phase estimator (3) was estimated in equation (5) by means of the sole sample information collected in the second phase, in equation (7) it was estimated by means of a regression estimator, exploiting the information provided by vegetation indexes. Therefore, in analogy with the variance estimator (6), we estimated the design-based sampling variance of the regression estimator (7) by means of
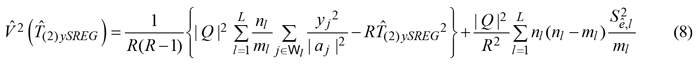
where
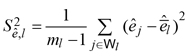
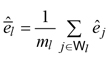
![]() Clearly, the two terms in equation (8) have analogous meaning of the two terms in equation (6).
Clearly, the two terms in equation (8) have analogous meaning of the two terms in equation (6).
Finally, we computed a nominal 95% confidence interval by means of ![]()
2.4 Simulation study
We checked the design-based performance of the proposed estimators by means of a simulation performed on a set of artificial populations of poplar plantations. The density, the size, the wood volume and the values of the auxiliary variable approximately resembled the results of some real assessments on poplar plantations in Northern Italy (Mattioli et al. 2019). Apart for these characteristics, the first part of the simulation (i.e. the generation of populations in accordance with several spatial patterns and the first phase of sampling) followed the simulation performed by Baffetta et al. (2011), regarding woodlots and tree-rows.
A quadrat of size 9 000 000 ha (side 300 km) was taken as the survey area. Populations of N = 20 000 poplar plantations (density of about 0.22 poplar plantations per 100 ha) were settled within the quadrat. For simplicity, the shape of poplar plantations was assumed to be circular. In order to consider several spatial patterns, the centers of plantations were distributed over the quadrat (a) completely at random, (b) in accordance with a clustered process in which 10 cluster centers were randomly distributed over the quadrat and for each cluster center 2000 centers were generated from a bivariate normal distribution centered at the cluster center and having independent marginal distributions with standard deviation equal to 25 km; (c) in accordance with a spatially-trended process in which the coordinates of centers were independent random variables of type ![]() with U uniformly distributed on (0,1). The centers of poplar plantations falling outside the quadrat were discarded and newly generated. Once the centers were located on the quadrat, circular poplar plantations were determined around each center with size generated from a lognormal distribution with expectation 1.29 ha and standard deviation 1.05 ha, in order to obtain populations with an average size of about 6 ha. Poplar plantations smaller than 0.5 ha, or partially lying outside the quadrat or overlapping previously generated poplar plantations were discarded and newly generated (see Fig. 3).
with U uniformly distributed on (0,1). The centers of poplar plantations falling outside the quadrat were discarded and newly generated. Once the centers were located on the quadrat, circular poplar plantations were determined around each center with size generated from a lognormal distribution with expectation 1.29 ha and standard deviation 1.05 ha, in order to obtain populations with an average size of about 6 ha. Poplar plantations smaller than 0.5 ha, or partially lying outside the quadrat or overlapping previously generated poplar plantations were discarded and newly generated (see Fig. 3).
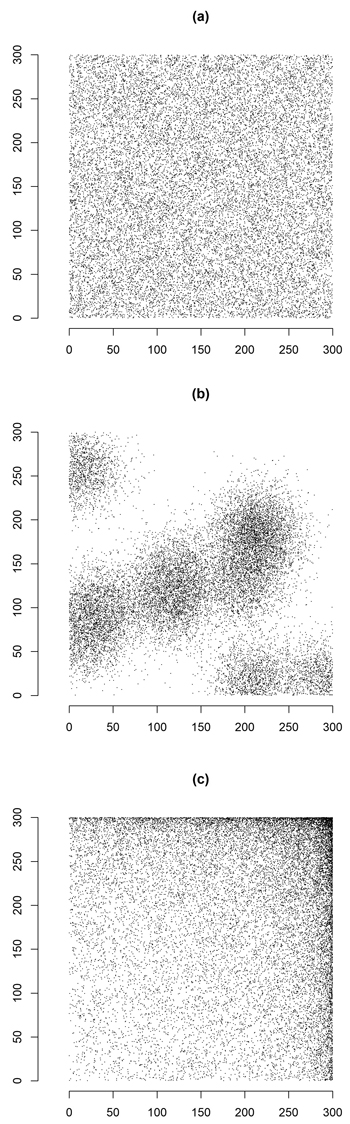
Fig. 3. Spatial distribution of populations of N = 20 000 circular poplar plantations artificially generated from random (a), clustered (b) and trended (c) spatial patterns.
For any poplar plantation, the wood volume was generated from the linear relationship
![]()
where the εj s were stochastic errors with zero expectation and standard deviation proportional to ![]() values. The coefficients αy and βy were chosen in such a way to give an average wood volume of about 900 m3 (150 m3 ha–1), while the proportionality constant of the error standard deviations was chosen in such a way to provide a correlation coefficient between wood volume and size of about 0.90. Tree volumes less than 0were discarded and newly generated. The linear relationship
values. The coefficients αy and βy were chosen in such a way to give an average wood volume of about 900 m3 (150 m3 ha–1), while the proportionality constant of the error standard deviations was chosen in such a way to provide a correlation coefficient between wood volume and size of about 0.90. Tree volumes less than 0were discarded and newly generated. The linear relationship
![]()
was adopted to generate the vegetation indexes to be exploited as auxiliary information in the linear regression estimator. The coefficients αx and βx were chosen in such a way to give an average vegetation index of about 4.20, while the εj s were stochastic errors with zero expectation and standard deviation such that to provide a correlation coefficient between wood density and vegetation index of about 0.60. Vegetation indexes less than 0were discarded and newly generated.
In the first phase we simulated TSS by partitioning the quadrat into R = 90 000 quadrats of size 100 ha, in order to ensure, in accordance with Baffetta et al. (2011), that quadrat size was relevantly larger than plantation sizes (100 ha against an average plantation size of 6 ha). The coverage estimate was computed using Eq. 1, randomly selecting a point in each quadrat and counting the number of points falling within poplar plantations. The corresponding estimate of the variance was computed from Eq. 2. All the poplar plantations containing at least one of the 90 000 sampling points were included in the first-phase sample.
In the second phase we simulated stratified sampling by partitioning the quadrat into L = 5 strata of size 2 340 000 ha, 2 160 000 ha, 1 710 000 ha, 2 070 000 ha and 720 000 ha, respectively. The dimensions of the strata were chosen to resemble those of the five administrative regions in the Padan Plain of Northern Italy (see the case study). Within each stratum, the 3% of poplar plantations selected in the first phase were selected by SRSWOR. Then we estimated the total wood volumes by means of Eq. 5 and Eq. 7, while the corresponding estimates of their variances were achieved using Eq. 6 and Eq. 8, respectively. From the variance estimates, the corresponding estimates of relative standard errors were achieved by the ratio of the square root of the variance estimate to the parameter estimate. Finally, for each parameter estimate, the nominal 95% confidence interval was computed by the estimate plus and minus 1.96 times the square root of the variance estimate.
For each artificial population, sampling and estimation were replicated 10 000 times, achieving the Monte Carlo distributions of estimators (1), (5) and (7) and of the corresponding variance estimators (2), (6) and (8). From the Monte Carlo distributions, expectations and mean squared errors of estimators were achieved together with expectations of the relative standard error estimators (ERSEE). From expectation and mean squared error of each estimator the relative bias (RB) and relative root mean squared error (RRMSE) were achieved. Finally, for each parameter, the actual coverage of the nominal 95% confidence intervals (AC95) was empirically determined as the percentage of times the simulated intervals contained the true parameter value.
2.5 Case study
We adopted the developed strategy for assessing poplar plantations in Northern Italy. The survey area was composed by five administrative Regions across the Padan Plain: Piedmont, Lombardy, Emilia-Romagna, Veneto and Friuli-Venezia Giulia, for a total extent of about 98 000 square kilometers. In the first phase, we adopted the TSS scheme of IUTI permanent national land-use pure-panel survey (Corona et al. 2012). The scheme was based on a grid of 360 000 semi-kilometer quadrats covering the whole Italian territory and as many sampling points randomly selected within each quadrat. Sampling points were photo-interpreted by high-resolution airborne imagery available for the whole area for the years 2014, 2015 and 2016, with geometric resolution <50 cm, and subsequently checked to obtain an error-free photo-interpretation using Google Maps images available for late summer 2017. We focused on the five northern regions that were covered by R = 390 643 quadrats. In those quadrats, sampling points classified as poplar plantations were 1736 (see Fig. 4). We then adopted estimators (1) and (2) to estimate the plantation area and its relative standard error.
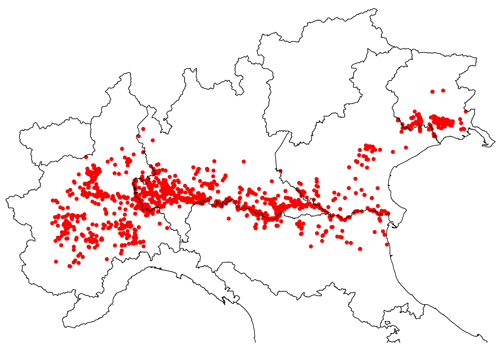
Fig. 4. Distribution of the 1736 sampling points falling in poplar plantations across the Padan Plain (Northern Italy).
In the second phase, a subset of 57 (about 3%) poplar plantations of the 1736 plantations selected in the first-phase sample was selected by means of stratified sampling with proportional allocation. Strata were represented by the five administrative Regions. The plantations selected in the second-phase sample were visited on the ground in May–July 2017. Each tree in each visited plantation was enumerated and the diameter at breast height and the tree height were recorded, along with the plantation age. We then reckoned the total wood volume of second-phase plantations as the sum of volumes of single trees that, in turn, were determined by means of allometric equations developed by Chiarabaglio and Coaloa (2002).
We estimated total wood volume on the basis of the sole sample information by means of Eq. 5. Sampling variance was estimated by means of Eq. 6.
Vegetation indexes were computed from ESA Sentinel-2 satellite mission, a constellation of two twin heliosynchronous satellites which provide freely available multispectral bands for the entire globe with a spatial resolution ranging between 10 m and 20 m (depending on the spectral band) and a revisit time of 5 days. The capabilities of Sentinel-2 spectral bands and vegetation indexes for wood volume estimation in Mediterranean forest ecosystems has been investigated by Chrysafis et al. (2017); Mura et al. (2018); Chrysafis et al. (2019). We downloaded all the Sentinel-2 images acquired in the time window 27 May 2017 – 10 June 2017, obtaining a stack of 43 Top of Atmosphere (TOA) Sentinel-2 images. The Sen2Cor algorithm (Louis et al. 2016) was used to calculate the Bottom of Atmosphere reflectance (BOA). This BOA dataset was used to create a cloud free image of the survey area. To do this, the spectral value of pixels covered by clouds was recomputed as the mean of values of cloud free pixels in the selected time window. Then, seven vegetation indices (Table 1) were computed from Sentinel-2 data taking into account previous studies (Chrysafis et al. 2017; Puletti et al. 2018; Chrysafis et al. 2019). The Pearson’s r correlation coefficient was used to investigate the relationships between the wood volume measured in the field and vegetation indices. Finally, the vegetation index with the best Pearson coefficient value was used as auxiliary information to estimate total wood volume by means of the regression estimator given by Eq. 7. Sampling variance was estimated by means of Eq. 8.
| Table 1. Vegetation indices derived from ESA Sentinel-2 satellite mission. | |||
| Vegetation index | Abbreviation | Formula | Reference |
| Simple Ratio 800/2170 | SR | Malthus et al. (1993) | |
| Mid-infrared Vegetation Index | MVI | Thenkabail et al. (2002) | |
| Normalized Difference Red Edge | NDRE | Hunt et al. (2011) | |
| Normalized Difference Vegetation Index | NDVI | Rouse et al. (1973) | |
| Normalized Difference Moisture Index | NDMI | Wilson and Sader (2002) | |
| Normalized Burn Ratio | NBR | Key and Benson (2005) | |
| Atmospherically Resistant Vegetational Index | ARVI | Thenkabail et al. (2002) | |
3 Results
Table 2 reports the percent values of RB, RRMSE, ERSEE, AC95 for each artificial population and each parameter. The coverage estimator proves to be unbiased and precise with RB always smaller than 0.06% and RRMSE invariably around 3%. The estimator of RRMSE turns out to be approximately unbiased and conservative, with a slight overestimation. The actual coverage of nominal 95% confidence intervals is always greater than the nominal level. Concerning the two alternative estimators of wood volume, they both result approximately unbiased, with RRMSE invariably below 10%. The RRMSE estimators are approximately unbiased, but except for the estimator based on the sole sample information under the clustered spatial pattern, they all provide moderate underestimation. As to the performance of nominal 95% confidence intervals, the actual coverage is always smaller than the nominal coverage of 95%, although it never turns out to be smaller than 92%. Finally, the regression estimator turns out to be invariably better than the estimator based on the sole sample information.
| Table 2. Relative bias (RB), relative root mean squared error (RRMSE), expectation of the relative standard error estimator (ERSEE) and actual coverage of the nominal 95% confidence intervals (AC95) of first-phase coverage estimator, second-phase estimator based on the sole sample information and second-phase linear regression estimator of wood volume for the three artificial populations of poplar plantations with random, clustered, and trended spatial distributions. | ||||
| Estimated attribute | Performance indexes | Random | Clustered | Trended |
| coverage | RB (%) | 0.05 | 0.06 | 0.01 |
| RRMSE (%) | 2.83 | 3.05 | 2.89 | |
| ERSEE (%) | 2.94 | 3.22 | 3.07 | |
| AC95(%) | 96.11 | 96.50 | 96.39 | |
| wood volume (sole sample information) | RB (%) | –2.46 | –2.06 | –2.10 |
| RRMSE (%) | 9.35 | 8.01 | 7.72 | |
| ERSEE (%) | 9.34 | 8.04 | 7.64 | |
| AC95(%) | 93.32 | 93.42 | 93.14 | |
| wood volume (linear regression estimator) | RB (%) | –2.54 | –2.18 | –2.16 |
| RRMSE (%) | 7.97 | 6.97 | 6.59 | |
| ERSEE (%) | 7.63 | 6.73 | 6.33 | |
| AC95(%) | 92.15 | 92.37 | 92.57 | |
Regarding the case study, the estimated area of poplar plantations in Northern Italy is 43 400 ha with an estimated relative error of 2.4% and nominal 95% confidence interval of 41 358–45 442. The estimate of total wood volume based on the sole sample information is 6 098 438 m3 with an estimated relative error of 11.7% and nominal 95% confidence interval of 4 699 944–7 496 932, while the linear regression estimate is 5 867 700 m3 with an estimated relative error of 10.7% and nominal 95% confidence interval of 4 637 126–7 098 274. The linear regression estimate of total wood volume was computed using the SR vegetation index from Sentinel-2 data, as among the tested vegetation indices SR has proved the best relationships with field wood volume measures (Table 3), albeit very similar correlation was found for the considered indices.
| Table 3. Pearson correlation coefficient between wood volume of poplar plantations and vegetation indices from Sentinel-2 imagery. | |
| Vegetation index (see Table 1) | Pearson coefficient |
| SR | 0.63 |
| MVI | 0.62 |
| NDRE | 0.60 |
| NDVI | 0.59 |
| NDMI | 0.59 |
| NBR | 0.59 |
| ARVI | 0.58 |
4 Discussion
We have developed a two-phase sampling strategy for large scale estimation of the total area and the total wood volume of fast-growing tree crops within agricultural farms. Regarding the scheme for locating points in the first phase, we adopted TSS instead of the most common systematic grid sampling (SGS), widely adopted in forest surveys over large scale (Tomppo et al. 2010). SGS as TSS involves covering the survey region by a grid of regular polygons of equal sizes, selecting a point at random in one polygon and the repeating it in the remaining polygons. From a practical point of view, SGS can be straightforwardly performed by a random shift of the grid that is superimposed onto the survey area, taking the nodes as sample points. For this reason, SGS has constituted a sort of standard design of wide application in environmental surveys (e.g. U.S. Environmental Protection Agency 2002). However, from a theoretical point of view, Barabesi and Franceschi (2011) argue about the superiority of TSS over SGS. While TSS invariably outperforms the benchmark scheme achieved by randomly and independently selecting point throughout the whole survey area (the so called URS from the acronym of uniform random sampling), in the presence of some spatial regularity, SGS may be even worse than URS. Moreover while TSS variance can be conservatively estimated in a very simple way using equation (2), no conclusion about the properties of (2) under SGS can be drawn. Finally, while TSS ensures the asymptotic normality of the resulting Monte Carlo estimator (1), normality cannot be proven under SGS.
Regarding the second-phase scheme for selecting and visiting a sub-sample of plantations selected in the first phase, the use of a stratified sample ensured the spreading of second-phase samples throughout plantation characteristics or throughout space or both, in accordance with second-phase stratification criteria. Moreover, the use of second-phase estimators (5) and (7) based on an approximation of the first-phase Horvitz-Thompson estimator (3) involved relevant simplifications in estimation without deteriorating the precision of the strategy when the size of the population units were much smaller than the polygon size (like in the considered case: few hectares against hundreds).
The strategy has been tested by a simulation study and applied in a case study on poplar plantations in Northern Italy. The linear regression estimator (7) turns out to be invariably better than the estimator based on the sole sample information (5), and, from a practical point of view, is proven fully feasible to be implemented and replicated, with reduced costs when exploiting freely available remotely sensed data like Sentinel-2 images.
From a practical point of view, it is important to stress that the first phase of the strategy proposed here coincides with the first phase performed in NFIs for those countries adopting TSS as first phase (e.g. Italy and USA). Therefore, in order to save time and resources it may be appealing to exploit the first phase of these inventories as the first phase of plantation surveys. In these cases, plantation surveys can benefit of the intensive sampling usually performed by NFIs in the first phase. In this sense, the proposed approach may represent a suitable reference for integrated NFI frameworks effectively supporting outside-forest resource monitoring and assessment.
The benefits of the strategy proposed here will be distinctively valuable for those countries and regions where short-rotation plantation forestry is well widespread, like e.g. France, Turkey, Iran, Spain, Brazil or China. Taking fixed the first-phase sample of plantations – possibly selected during a NFI – the proposed second-phase sampling strategy can allow to update information on a short time; it has the advantage of being rapid and simple to be carried out, being particularly suited for fast-growing plantations, which rapidly alternate on agricultural lands, making conventional 5–10 years periodic inventory information temporally obsolete.
Acknowledgements
The study was financially supported by the Research Project PRECISIONPOP (Sistema di monitoraggio multiscalare a supporto della pioppicoltura di precisione nella Regione Lombardia) funded by the Lombardy Region, Italy, grant number: E86C18002690002.
References
Alam M.B., Shahi C., Pulkki R. (2014). Economic impact of enhanced forest inventory information and merchandizing yards in the forest product industry supply chain. Socio-Economic Planning Sciences 48(3): 189–197. https://doi.org/10.1016/j.seps.2014.06.002.
Baffetta F., Fattorini L., Corona P. (2011). Estimation of woodlot and tree row attributes in large-scale forest inventories. Environmental and Ecological Statistics 18: 147–167. https://doi.org/10.1007/s10651-009-0125-0.
Barabesi L., Franceschi S. (2011). Sampling properties of spatial total estimators under tessellation stratified designs. Environmetrics 22(3): 271–278. https://doi.org/10.1002/env.1046.
Barabesi L., Franceschi S., Marcheselli M. (2012). Properties of design-based estimation under stratified spatial sampling with application to canopy cover estimation. Annals of Applied Statistics 6(1): 210–228. https://doi.org/10.1214/11-AOAS509.
Chiarabaglio P.M., Coaloa D. (2002). Valutazione qualitativa e quantitativa del pioppeto maturo in piedi. [Qualitative and quantitative assessment of standing poplar plantation]. L’Informatore Agrario 41: 25–27.
Chrysafis I., Mallinis G., Siachalou S., Patias P. (2017). Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sensing Letters 8(6): 508–517. https://doi.org/10.1080/2150704X.2017.1295479.
Chrysafis I., Mallinis G., Tsakiri M., Patias P. (2019). Evaluation of single-date and multi-seasonal spatial and spectral information of Sentinel-2 imagery to assess growing stock volume of a Mediterranean forest. International Journal of Applied Earth Observation and Geoinformation 77: 1–14. https://doi.org/10.1016/j.jag.2018.12.004.
Corona P., Barbati A., Tomao A., Bertani R., Valentini R., Marchetti M., Fattorini L., Perugini L. (2012). Land use inventory as framework for environmental accounting: an application in Italy. iForest 5(4): 204–209. https://doi.org/10.3832/ifor0625-005.
FAO (2015). Global forest resources assessment 2015. Food and Agriculture Organization of United Nations, Rome, Italy.
Fattorini L., Marcheselli M., Pisani C. (2006). A three-phase sampling strategy for large-scale multiresource forest inventories. Journal of Agricultural, Biological and Environmental Statistics 11: 1–21. http://dx.doi.org/10.1198/108571106X130548.
Gregoire T.G., Valentine H.T. (2008) Sampling strategies for natural resources and the environment. Chapman & Hall, New York.
Hunt Jr E.R., Daughtry C.S.T., Eitel J.U.H., Long D.S. (2011). Remote sensing leaf chlorophyll content using a visible band index. Agronomy Journal 103(4): 1090–1099. https://doi.org/10.2134/agronj2010.0395.
Key C.H., Benson N.C. (2005). Landscape assessment: remote sensing of severity, the Normalized Burn Ratio. In: Lutes D.C. (eds.). FIREMON: rire effects monitoring and inventory system. General Technical Report, RMRSGTR-164-CD:LA1-LA51. USDA Forest Service, Rocky Mountain Research Station.
Louis J., Debaecker V., Pflug B., Main-Knorn M., Bieniarz J., Müller-Wilm U., Cadau E., Gascon F. (2016). Sentinel-2 L2A processor Sen2Cor.
Malthus T.J., Andrieu B., Danson F.M., Jaggard K.W., Steven M.D. (1993). Candidate high spectral resolution infrared indices for crop cover. Remote Sensing of Environment 46(2): 204–212. https://doi.org/10.1016/0034-4257(93)90095-f.
Mattioli W., Puletti N., Coaloa D., Rosso L., Chianucci F., Grotti M., Corona P.(2019). INARBO.IT: inventario degli impianti di arboricoltura da legno in Italia.[INARBO.IT: Inventory of arboriculture plantations in Italy]. Sherwood 239:7–10.
Mura M., Bottalico F., Giannetti F., Bertani R., Giannini R., Mancini M., Orlandini S., Travaglini D., Chirici G. (2018). Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. International Journal of Applied Earth Observation and Geoinformation 66: 126–134. https://doi.org/10.1016/j.jag.2017.11.013.
Payn T., Carnus J.-M., Freer-Smith P., Kimberley M., Kollert W., Liu S., Orazio C., Rodriguez L., Silva L.N., Wingfield M.J. (2015). Changes in planted forests and future global implications. Forest Ecology and Management 352: 57–67. https://doi.org/10.1016/j.foreco.2015.06.021.
Puletti N., Chianucci F., Castaldi C. (2018). Use of Sentinel-2 for forest classification in Mediterranean environments. Annals of Silvicultural Research 42(1): 32–38. https://doi.org/10.12899/asr-1463.
Rouse J.W., Haas R.H., Schell J.A., Deering D.W. (1973). Monitoring the vernal advancement and retrogradation (green wave effect) of natural vegetation. Progress Report RSC 112:1978-1. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19730017588.pdf.
Särndal C.E., Swensson B., Wretman J. (1992). Model assisted survey sampling. Springer, New York.
Stevens Jr. D.L. (1997). Variable density grid-based sampling designs for continuous spatial populations. Environmetrics 8(3): 167–195. https://doi.org/10.1002/(SICI)1099-095X(199705)8:3<167::AID-ENV239>3.0.CO;2-D.
Thenkabail P.S., Smith R.B., De Pauw E. (2002). Evaluation of narrowband and broadband vegetation indices for determining optimal hyperspectral wavebands for agricultural crop characterization. Photogrammetric Engineering and Remote Sensing 68: 607–621.
Tomppo E., Gschwantner T., Lawrence M., McRoberts R.E. (eds.) (2010). National forest inventories: pathways for common reporting. Springer, New York. https://doi.org/10.1007/978-90-481-3233-1.
U.S. Environmental Protection Agency (2002). Guidance on choosing a sampling design for environmental data collection. EPAQA/G-5S, Washington DC.
Wilson E.H., Sader S.A. (2002). Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sensing of Environment 80(3): 385–396. https://doi.org/10.1016/s0034-4257(01)00318-2.
Total of 26 references.

