Empirical equations for estimating aboveground biomass of Betula pendula growing on former farmland in central Poland
Bronisz K., Strub M., Cieszewski C., Bijak S., Bronisz A., Tomusiak R., Wojtan R., Zasada M. (2016). Empirical equations for estimating aboveground biomass of Betula pendula growing on former farmland in central Poland. Silva Fennica vol. 50 no. 4 article id 1559. https://doi.org/10.14214/sf.1559
Highlights
- We developed equations for aboveground biomass components of young silver birch stands on post-agricultural lands in central Poland for single tree level
- Simplified equations were based exclusively on diameter at ground level or breast height, while expanded ones were based on the appropriate diameter and tree height
- For large trees, diameter at breast height is a more appropriate explanatory variable than diameter at ground level
- Biomass estimations based on models from neighboring countries were consistent with our results.
Abstract
We determined empirical models for estimating total aboveground as well as stem, branches, and foliage dry biomass of young (age up to 16 years) silver birch (Betula pendula Roth.) growing on the post-agricultural lands. Two sets of allometric models for trees with a height below or above 1.3 m (small and large trees respectively) were developed. Simplified models were elaborated based exclusively on appropriate tree diameter (diameter at ground level for small trees, diameter at breast height for large trees), while expanded models also included tree height. Total aboveground biomass was estimated as the sum of biomass of all tree components. To assure additivity of the developed equations, the seemingly unrelated regression approach for the final model fitting was used. Expanded models in both tree groups were characterized by a better fit to the data (R2 for total aboveground biomass for small and large trees equaled 0.8768 and 0.9752, respectively). Diameter at breast height appeared to be a better predictor than diameter at ground level – simplified models had better fit for large trees (R2 for total aboveground biomass equals 0.9611) than for small ones (R2 = 0.7516). The developed equations provide biomass predictions consistent with available Latvian, Estonian, Finnish, Swedish, and Norwegian models for silver birch.
Keywords
silver birch;
simplified and expanded models;
seemingly unrelated regression
-
Bronisz,
Laboratory of Dendrometry and Forest Productivity, Faculty of Forestry, Warsaw University of Life Sciences – SGGW, Nowoursynowska 159, 02-787 Warsaw, Poland
E-mail
karol.bronisz@wl.sggw.pl

- Strub, Warnell School of Forestry and Natural Resources, University of Georgia, Athens, GA, 30605, USA E-mail strub@mcfns.com
- Cieszewski, Warnell School of Forestry and Natural Resources, University of Georgia, Athens, GA, 30605, USA E-mail thebiomat@gmail.com
- Bijak, Laboratory of Dendrometry and Forest Productivity, Faculty of Forestry, Warsaw University of Life Sciences – SGGW, Nowoursynowska 159, 02-787 Warsaw, Poland E-mail szymon.bijak@wl.sggw.pl
- Bronisz, Laboratory of Dendrometry and Forest Productivity, Faculty of Forestry, Warsaw University of Life Sciences – SGGW, Nowoursynowska 159, 02-787 Warsaw, Poland E-mail agnieszka.bronisz@wl.sggw.pl
- Tomusiak, Laboratory of Dendrometry and Forest Productivity, Faculty of Forestry, Warsaw University of Life Sciences – SGGW, Nowoursynowska 159, 02-787 Warsaw, Poland E-mail robert.tomusiak@wl.sggw.pl
- Wojtan, Laboratory of Dendrometry and Forest Productivity, Faculty of Forestry, Warsaw University of Life Sciences – SGGW, Nowoursynowska 159, 02-787 Warsaw, Poland E-mail rafal.wojtan@wl.sggw.pl
- Zasada, Laboratory of Dendrometry and Forest Productivity, Faculty of Forestry, Warsaw University of Life Sciences – SGGW, Nowoursynowska 159, 02-787 Warsaw, Poland E-mail michal.zasada@wl.sggw.pl
Received 2 February 2016 Accepted 20 June 2016 Published 1 July 2016
Views 213343
Available at https://doi.org/10.14214/sf.1559 | Download PDF

1 Introduction
Recent socio-economic changes in Central and Eastern Europe have resulted in abandonment of farming in many rural areas. These areas are frequently subjected to rapid secondary succession of pioneer forest tree species, such as silver birch (Betula pendula Roth.) (Karlsson et al. 1998; Zając and Gil 2003; Uri et al. 2007). The scale of this phenomenon is significant in many regions; yet, its extent and ecological and economic consequences are still largely unknown (Szwagrzyk 2004). In Poland, there are only rough estimations about the area of silver birch secondary succession on abandoned farmlands, covering around 900 000 hectares (Krawczyk 2015), which corresponds to almost 10% of contemporary Polish forests area.
The large scale of silver birch secondary succession on abandoned farmlands can play an important role in atmospheric carbon sequestration, as increasing afforestation and the intensity of forest management are considered the most effective ways of offsetting CO2 emissions. In recent decades, issues related to climate change have become more and more frequently the subject of both discussions between policy makers and scientific research activities around the world. One of the examples is the world’s strongest climate-energy policy that was agreed upon by the European Union leaders (European Council conclusions 2014). Its objective assumes that within the European Union, at least 27% of the energy demand is being covered by renewable energy sources by 2030. Forest ecosystems, including secondary succession on abandoned farmlands, are an important source of biomass and make a significant contribution to the global carbon budget and the mitigation of climate change (van Kooten et al. 2004; Fahey et al. 2009; Rittenhouse and Rissman 2012). In addition, management of natural silver birch ecosystems can result in considerable economic impacts by providing biomass for energy production and wood for the timber industry (Elowson 1996). Therefore, analysis of biomass and carbon sequestration and modeling growth rates and yields of such ecosystems are important research challenges.
For a number of years, many countries have been making commitments to increase biomass production in forest ecosystems for bio-energy production and carbon sequestration. A significant number of publications consider this issue in different forest types of North America (Birdsey 1992; Brown et al. 1999; Van Tuyl et al. 2005), tropical forests (Detwiler and Hall 1988; Alves et al. 2010; Ribeiro et al. 2011), and in Europe (Zasada et al. 2009; Skovsgaard and Nord-Larsen 2012; González-García et al. 2013).
An exemplary approach to estimate carbon sequestration in forest ecosystems is the assessment of different carbon pools (especially in case of wood) and an evaluation of their physical characteristics, such as moisture and specific gravity. The results of such estimations are used to determine biomass of tree components and, consequently, biomass and the carbon accumulation in the studied areas. A common procedure is also the weighting all components in the field and to apply moisture content in order to determine dry weight. The main advantages of such an approach are the high accuracy of the estimation of the tree component and its high flexibility in terms of modeling carbon sequestration at the stand level. In this scenario, total aboveground biomass and/or biomass of each tree component is determined as a function of tree characteristics, such as diameter at breast height (Muukkonen 2007), diameter and height (Ter-Mikaelian and Korzukhin 1997) and diameter at ground level (Kuznetsova et al. 2011), tree height (Adegbidi et al. 2002), diameter at ground level and tree height (Pajtík et al. 2011), diameter at 15 cm from the stem base, average height and number of stems (Lupi et al. 2015) in case of young stands or tree equivalent diameter at 5 cm above the ground for young coppices (Cotillas et al. 2016).
Biomass of silver birch stands is a vital theme in Fennoscandia and the Baltic Sea region. Smith et. al. (2014; 2016) suited regional allometric biomass functions for Norwegian conditions. In Finland, Mälkönen (1977) analyzed total aboveground biomass production in 40-year-old silver birch stands, Ferm (1993) evaluated the potential of silver birch for biomass production, Repola (2008) developed biomass equations, while Tahvanainen and Forss (2008) proposed individual tree models for the biomass distribution in tree crowns. Johansson (1999; 2007) elaborated biomass equations for silver birch stands growing on abandoned farmland in Sweden. Marklund (1988) analyzed this tree species for a wide range of combinations of sites and stand ages, while Kuznetsova et al. (2011) and Uri et al. (2012) performed similar studies in Estonia and Daugaviete et al. (2008) in Latvia.
In Poland, studies on biomass and carbon accumulation were focused mainly on Scots pine (Pinus sylvestris L.). Thus, for example, Oleksyn et al. (1999) analyzed variability of growth and the distribution of above- and belowground biomass in young stands of 19 provenances. Allocation of aboveground biomass in stands up to an age of 20 years was also assessed by Jagodziński et al. (2014). Socha and Wężyk (2004) as well as Zasada et al. (2008) studied aboveground biomass of this tree species in a greater age range. Recent studies have also included other tree species, such as black alder (Alnus glutinosa (L.) Gaertn.) (Ochał et al. 2014). So far, biomass of silver fir stands in Poland was analyzed only by Bijak et al. (2013) and Zasada et al. (2014).
The general objective of this study was to develop empirical equations of total aboveground, stem, branches and foliage biomass of young, naturally regenerated, silver birch trees growing on abandoned farmlands in central Poland. The specific primary objectives were to create two sets of models for two groups of trees: i) simplified models based on the diameter at ground level for small trees (height below 1.3 m) and diameter at breast height for large trees (height above 1.3 m) and ii) expanded models based on diameter at ground level and height for small trees and diameter at breast height and height for large trees.
The specific secondary objectives of this study were to analyze influence of applied explanatory variables (diameter at ground level, diameter at breast height, and height) and compare developed models to estimates obtained with equations from neighboring countries.
2 Materials and data
2.1 Study sites
Data for this study were collected in 20 pure silver birch stands growing on post-agricultural lands in the Mazowieckie province, central Poland (52°21´–51°24´N, 20°39´–21°26´E, Table 1). The former farmland status and the cessation of agricultural use were checked and confirmed by the owners and local administration. All sampled stands originated from natural regeneration after the cessation of farming practices. No silvicultural treatments were applied to any of these stands prior to sampling.
| Table 1. Average stand age (a [years]), average study plot area (A [ha]), stocking (N [trees ha–1]), basal area at breast height (BA [m2 ha–1]), average diameter at breast height (DBH [cm]), mean height (H [m]), and growing stock (V [m3 ha–1]) of the study sites. | |||||||
| a | A | N | BA | DBH | H | V | |
| Min | 2 | 0.0002 | 2987 | - | - | 0.15 | 0.61 |
| Max | 14 | 0.0500 | 1555556 | 51.49 | 8.40 | 10.65 | 263.00 |
| Mean | 8 | 0.0135 | 144849 | 12.09 | 3.01 | 4.70 | 60.66 |
| Median | 7 | 0.0061 | 33194 | 10.50 | 1.55 | 3.23 | 35.53 |
| Standard deviation | 4 | 0.0148 | 345547 | 13.31 | 2.91 | 3.93 | 71.93 |
All study sites were located in a transition zone from the maritime to the continental type within temperate climate (Martyn 2000). Mean annual temperature reaches 6 to 8 °C. January is the coldest month with average temperature slightly below –2 °C. The highest temperature is recorded in July and ranges from 16 to 18 °C. The investigated region has generally poor precipitation and occasionally suffers from droughts. The average annual rainfall rarely exceeds 550 to 600 mm (Martyn 2000). Soils developed on glacio-fluvial sands, glacial tills, clays, as well as peats. In general, these soils are rather nutrient poor and relatively unfertile.
2.2 Material collection and preparation
At each plot, we randomly chose ten trees from the range of diameters in the stand. Felled trees were section-wise (1 m section length) measured for their volume and divided into the components: stems, foliage, and branches. All parts of each individual tree were weighed in the field using portable scales (precision 0.1 g). Samples of each of the components (stem discs in the middle of each 1 m section, random samples of branches and foliage) from every tree were taken to determine the relationship between fresh and dry biomass. The samples were oven-dried at 105 °C (Samuelsson et al. 2006) until they reached a constant weight. The dry biomass of various components was calculated for each tree on the basis of corresponding fresh to dry mass ratios (Snowdon et al. 2002).
2.3 Tree data
Measurements were performed on 200 trees in total. During the initial analyses, outliers were removed and for further calculations, 189 trees were taken into account. Assessment of outlier trees was carried out on the basis of graphical behavior (Belsley et al. 1980) and evaluation of the contribution of the individual biomass components. Presumably, these trees were growing under specific conditions such as forest gaps or local soil and water conditions. In total, 148 of the analyzed trees were taller than 1.3 m and their diameter at breast height (dbh) could be measured (those trees were referred to as “large trees”, Table 2). The remaining 41 trees, which were smaller than 1.3 m, were included into a group called “small trees” (Table 2).
| Table 2. Age (a [years]), diameter at ground level (d0 [cm]), diameter at breast height (dbh [cm]), height (h [m]), total aboveground (AB), stem (ST), branches (BR), and foliage (FL) dry biomass [kg] of the sampled trees. | ||||||||
| Small trees | ||||||||
| a | d0 | h | AB | ST | BR | FL | ||
| Min | 1 | 0.23 | 0.26 | 0.0007 | 0.0004 | 0 | 0.0003 | |
| Max | 5 | 1.30 | 1.27 | 0.0540 | 0.0286 | 0.0126 | 0.0143 | |
| Mean | 3 | 0.77 | 0.71 | 0.0145 | 0.0066 | 0.0029 | 0.0050 | |
| Median | 3 | 0.72 | 0.68 | 0.0095 | 0.0042 | 0.0019 | 0.0032 | |
| Standard deviation | 1 | 0.26 | 0.28 | 0.0130 | 0.0066 | 0.0029 | 0.0042 | |
| Large trees | ||||||||
| a | d0 | dbh | h | AB | ST | BR | FL | |
| Min | 3 | 0.90 | 0.10 | 1.41 | 0.0183 | 0.0128 | 0.0034 | 0.0021 |
| Max | 16 | 15.80 | 9.70 | 13.08 | 24.045 | 20.6267 | 4.2564 | 1.1328 |
| Mean | 9 | 5.78 | 3.22 | 5.57 | 3.5891 | 2.9820 | 0.4431 | 0.1740 |
| Median | 9 | 5.15 | 2.90 | 4.85 | 1.4377 | 1.0776 | 0.2414 | 0.1083 |
| Standard deviation | 4 | 3.41 | 2.17 | 2.96 | 5.4407 | 4.6867 | 0.6440 | 0.2114 |
3 Methods
3.1 Biomass models
All biomass components were estimated based on models found in the literature, which were divided into two groups. The first one consisted of eight models [Eq. 1–8] based exclusively on diameter at ground level (d0) for small and large trees and diameter at breast height (dbh) for large trees (e.g. Johansson 2007; Pajtík et al. 2008; Teobaldelli et al. 2009; Uri et al. 2012). The other group consisted of six models [Eq. 9–14] based on d0 or dbh and height (Zianis et al. 2005; Cienciala et al. 2006; Zasada et al. 2008; Ochał et al. 2014):



where:
y – each dry biomass component [kg],
x – diameter at ground level (small trees) or diameter at breast height (large trees) [cm],
h – tree height [m],
a, b, c – model parameters.
3.2 Model fitting and comparison
All models were fit to data separately for stem, branches and foliage biomass and compared based on the following goodness-of-fit measures: coefficient of determination (R2), residual standard error (RSE) and Schwarz’s Bayesian information criterion (BIC). We also analyzed statistical significance of model parameters and normality of residuals based on Shapiro-Wilk test. In the final step, the best simplified and extended models for small and large trees were used as a base for Seemingly Unrelated Regression (SUR). This approach enabled fulfillment of the logical assumption that the sum of the estimated biomass values of tree parts (stem, branches, and foliage) matches the estimated total aboveground biomass, assuring additivity of the biomass equations (Kozak 1970; Chiyenda and Kozak 1984; Cunia and Briggs 1984). Despite the limitations caused by the additivity constraint, assuming homoscedasticity of variance, SUR estimators have smaller variances and are more effective than those constructed using alternative estimation methods (Zellner 1962; Parresol 1999; Bi et al. 2010). To assure the homoscedasticity of variance during SUR analyses model parameters, weighting by the inverse of diameter (d0 for small and dbh for large trees) square root was applied (Carvalho and Parresol 2003; Balboa-Murias et al. 2006).
Both predicted and measured total aboveground biomass values for large trees from this study were compared with predictions obtained by Baltic and Scandinavian models from the literature. Predicted total aboveground biomass was analyzed using graphical behavior of models from this study (both simplified and expanded) and reference ones from the literature. Measured total aboveground biomass was tested based on coefficient of determination (R2) and residual standard error (RSE), achieved by compared models from the literature. We also assessed correlation between analyzed models. In case of simplified models, Swedish (Johansson 1999), Estonian (Varik et al. 2009; Uri et al. 2012), and Latvian (Liepiņš 2013) solutions were analyzed. Repola’s (2008) model for Finland and the solution for Norway from Smith et al. (2014) allowed us to compare the expanded models. For convenient analysis, all included models were numbered with Roman numerals (Fig. 3).
Calculations and analyses were performed using RStudio (RStudio Team 2015), packages: nls (Bates and Watts 2007) and ggplot2 (Wickham 2009) in R software (R Development Core Team 2008) and PROC MODEL in SAS (SAS 9.1.3 Help and Documentation 2002).
4 Results
4.1 Model fitting
Based on the goodness-of-fit measures and model parameters accuracy, the most appropriate simplified and expanded equations to estimate stem, branches, and foliage biomass for small and large trees were chosen separately (Table 3). Models number 6 (simplified), 10, and 12 (expanded) presented the best goodness-of-fit statistics in most cases. The expanded models for both small and large trees are characterized by a better fit to data than the simplified ones (for foliage, coefficient of determination and residual standard error were almost the same for both model types). Both simplified and expanded models for large trees based on dbh are characterized by a better fit then models based on d0 (except simplified models for branches). Also, in some cases (p-value > 0.05), model residuals followed normal distribution (Table 3).
| Table 3. Goodness-of-fit measures (R2 = coefficient of determination, RSE = residual standard error, BIC = Schwarz’s Bayesian information criterion, p-value = Shapiro-Wilk test result for residuals normality) for the best simplified (S) and expanded (E) models for estimating stem (ST), branches (BR), and foliage (FL) dry biomass in analyzed tree groups. | ||||||
| Model type and number | R2 | RSE | BIC | p-value | ||
| Small trees (S for d0, E for d0 and h) | ||||||
| S | 6 | ST | 0.6476 | 0.0040 | –327.49 | 0.002 |
| 6 | BR | 0.6528 | 0.0017 | –396.07 | 0.018 | |
| 1 | FL | 0.7003 | 0.0023 | –371.38 | 0.648 | |
| E | 10 | ST | 0.9007 | 0.0021 | –375.72 | <0.0001 |
| 13 | BR | 0.7165 | 0.0015 | –408.09 | 0.087 | |
| 9 | FL | 0.7018 | 0.0023 | –371.58 | 0.818 | |
| Large trees (S for dbh, E for dbh and h) | ||||||
| S | 6 | ST | 0.9625 | 0.9110 | 405.40 | <0.0001 |
| 1 | BR | 0.8105 | 0.2813 | 57.56 | <0.0001 | |
| 5 | FL | 0.7556 | 0.1052 | –229.55 | <0.0001 | |
| E | 10 | ST | 0.9826 | 0.6226 | 296.69 | <0.0001 |
| 12 | BR | 0.8267 | 0.2700 | 49.36 | <0.0001 | |
| 12 | FL | 0.7681 | 0.1025 | –237.34 | 0.004 | |
| Large trees (S for d0, E for d0 and h) | ||||||
| S | 6 | ST | 0.9270 | 1.2709 | 503.94 | <0.0001 |
| 1 | BR | 0.8196 | 0.2745 | 50.33 | <0.0001 | |
| 5 | FL | 0.6865 | 0.1192 | –192.71 | <0.0001 | |
| E | 10 | ST | 0.9733 | 0.7706 | 359.82 | <0.0001 |
| 12 | BR | 0.8196 | 0.2754 | 55.29 | <0.0001 | |
| 12 | FL | 0.6866 | 0.1191 | –192.76 | <0.0001 | |
4.2 Seemingly Unrelated Regression
Total aboveground biomass was not included in the system of equations as it is explicitly related to the biomass of tree components as their sum. First, models for small trees were fitted. Estimates for all biomass components for simplified models were obtained as a function of d0, whereas for the expanded ones, as a function of d0 and height (h) (Table 4). Comparisons of residual distribution for analyzed models for small trees are shown based on the example for total aboveground biomass (Fig. 1).
| Table 4. Parameters (a, b, c) with their standard errors (SE) and goodness-of-fit measures (R2 = coefficient of determination, RSE = residual standard error, p-value = Shapiro-Wilk test result for residuals normality) for the final simplified (S) and expanded (E) models for small trees. All parameters are statistically significant at the significance level 0.05. | |||||||||||
| Model type and number | a | SE | b | SE | c | SE | R2 | RSE | p-value | ||
| S | 6+6+1 | AB | - | - | - | - | - | - | 0.7516 | 0.0068 | 0.3683 |
| 6 | ST | –1.91375 | 0.2144 | –2.52269 | 0.2165 | - | - | 0.6653 | 0.0039 | 0.0506 | |
| 6 | BR | –2.76320 | 0.2066 | –2.51018 | 0.2085 | - | - | 0.6646 | 0.0017 | 0.0863 | |
| 1 | FL | 0.00807 | 0.0003 | 2.26422 | 0.1880 | - | - | 0.6982 | 0.0024 | 0.8324 | |
| E | 10+13+9 | AB | - | - | - | - | - | - | 0.8768 | 0.0048 | 0.5060 |
| 10 | ST | 0.01291 | 0.0004 | 1.28721 | 0.1880 | 1.875852 | 0.1935 | 0.9057 | 0.0021 | 0.0007 | |
| 13 | BR | 0.00537 | 0.0002 | - | - | - | - | 0.7286 | 0.0016 | 0.1216 | |
| 9 | FL | 0.00881 | 0.0004 | 0.77260 | 0.0619 | - | - | 0.7030 | 0.0024 | 0.9626 | |
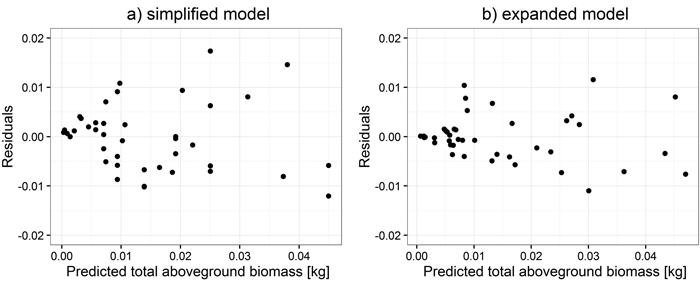
Fig. 1. Distribution of weighted residuals of simplified (a) and expanded (b) models for small trees.
Secondly, parameters for large trees were estimated. Simplified model parameter estimates for all biomass components were obtained as a function of dbh, whereas for expanded models, estimation was based on a function of dbh and h (Table 5). Those models were chosen because of their better fit to data than those based on d0. Comparisons of residual distribution for analyzed models for large trees are shown based on the example of total aboveground biomass (Fig. 2).
| Table 5. Parameters (a, b, c) with their standard errors (SE) and goodness-of-fit measures (R2 = coefficient of determination, RSE = residual standard error, p-value = Shapiro-Wilk test result for residuals normality) for the final simplified (S) and expanded (E) models for large trees. All parameters are statistically significant at the significance level 0.05. | |||||||||||
| Model type and number | a | SE | b | SE | c | SE | R2 | RSE | p-value | ||
| S | 6+1+5 | AB | - | - | - | - | - | - | 0.9611 | 0.6997 | <0.0001 |
| 6 | ST | 4.55434 | 0.0556 | –14.57160 | 0.3815 | - | - | 0.9616 | 0.5930 | <0.0001 | |
| 1 | BR | 0.02126 | 0.0048 | 2.176631 | 0.1136 | - | - | 0.8235 | 0.1753 | <0.0001 | |
| 5 | FL | 0.03489 | 0.0200 | 0.007996 | 0.0043 | –2.09076 | 0.2573 | 0.7460 | 0.0713 | <0.0001 | |
| E | 10+12+12 | AB | - | - | - | - | - | - | 0.9752 | 0.5612 | <0.0001 |
| 10 | ST | 0.02606 | 0.0032 | 1.705293 | 0.0620 | 1.163906 | 0.0814 | 0.9820 | 0.4063 | <0.0001 | |
| 12 | BR | 0.12882 | 0.0399 | 0.037619 | 0.0023 | –0.04669 | 0.0126 | 0.8379 | 0.1683 | <0.0001 | |
| 12 | FL | 0.06611 | 0.0180 | 0.011822 | 0.0010 | –0.01331 | 0.00553 | 0.7561 | 0.0698 | 0.0046 | |
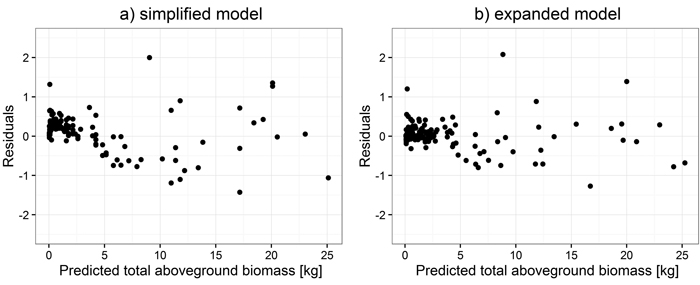
Fig. 2. Distribution of weighted residuals of simplified (a) and expanded (b) models for large trees.
4.3 Comparison with other models
Predicted total aboveground biomass for large trees based on the Johansson (1999, model II) and Varik et al. (2009, model III) models give similar values of total aboveground biomass compared to those determined by simplified models for large trees from this study (Fig. 3a, model I). Application of the Uri et al. (2012) model, created for young silver birch stands from Järvselja in Estonia (model IV), to the data from central Poland leads to an explicit underestimation of total aboveground biomass, whereas the Estonian model for older stands from Kambja (model V) fits best (Fig. 3a). This is also confirmed in the assessment of compared model fits to measured total aboveground biomass (Table 6). Goodness-of-fit (Table 6) and compared expanded model application for three levels of all large tree heights (minimum, mean and maximum height, Table 2), shown in Fig. 3b, explained that predicted biomass values based on the Norwegian model (Smith et al. 2014, model IX) is more consistent with predicted and measured total aboveground biomass from this study than predicted biomass values based on the Finnish model (Repola 2008, model VIII).
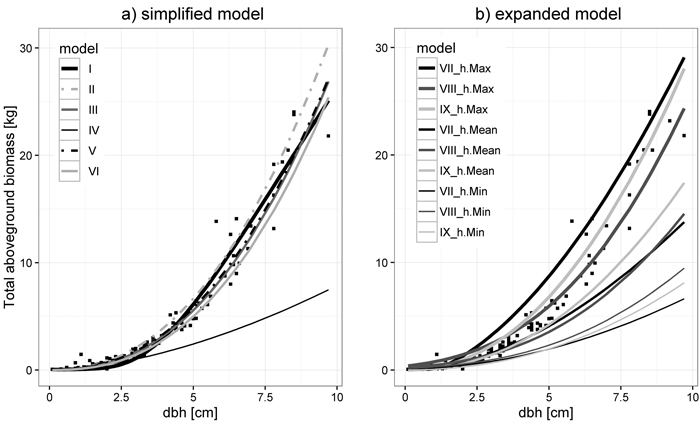
Fig. 3. Comparison to models from literature for large trees (black squares – measured total aboveground biomass). Simplified models (a): I – from this study (Table 4), II – Johansson (1999), III – Varik et al. (2009), IV and V Uri et al. (2012) models from Järvselja and Kambja respectively, VI – Liepiņš (2013). Expanded models (b): VII – form this study (Table 5), VIII – Repola (2008), IX – Smith et al. (2014) applied for minimum (h.Min), mean (h.Mean) and maximum (h.Max) height for all large trees.
| Table 6. Goodness-of-fit measures (R2 = coefficient of determination, RSE = residual standard error) for compared models (numbers defined in Fig. 3). | |||||||
| Model type and number | Simplified | Expanded | |||||
| II | III | IV | V | VI | VIII | IX | |
| R2 | 0.9395 | 0.9609 | 0.3249 | 0.9619 | 0.9474 | 0.9236 | 0.9698 |
| RSE | 1.3432 | 1.0799 | 4.4856 | 1.0656 | 1.2523 | 1.5141 | 0.9513 |
Both Estonian simplified models (Uri et al. 2012), representing the best (model V) and the worst fit (model IV, Table 6), as well as two expanded ones (Repola 2008; Smith et al. 2014, model VIII and IX, respectively), were characterized by different correlation with models from this study (Fig. 4). In the case of simplified models, the lowest correlation coefficient was identified for the Estonian model IV from Järvselja (0.3249), while the highest was obtained for model V (0.9619). For expanded models, values of correlation coefficients were similar and equaled 0.9979 for model VIII and 0.9958 for model IX.
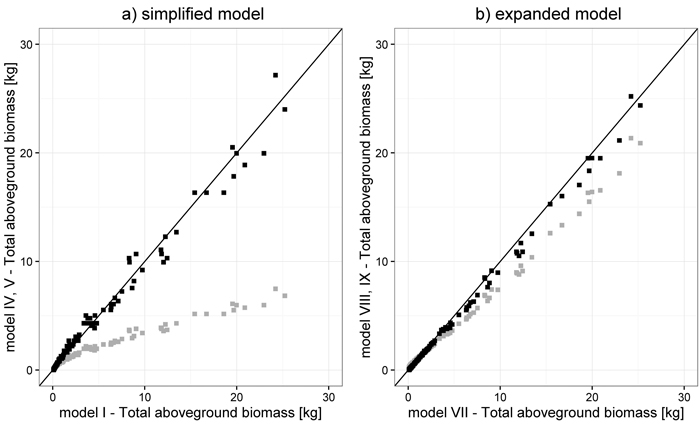
Fig. 4. Correlation between total aboveground biomass estimated with models developed in this study (model I and model VII) and estimated with the worst and best fitting models from the literature: model IV (grey) and model V (black), respectively, for simplified models (a) and model VIII (grey) and model IX (black), respectively, for expanded models (b) (model numbers are defined in Fig. 3).
5 Discussion
Forest management consists of many tools, including growth and yield models, necessary for prediction and compilation of the inventory data. In this paper, we present biomass models for young silver birch trees and their different components. We proposed two sets of models for small trees of a height below 1.3 m and adequate sets for large trees with dbh greater than zero (height above 1.3 m). The first set was exclusively based on tree diameter, while the other also used tree height as an additional independent variable.
The majority of so-far developed allometric equations model biomass as a function of dbh only, since this parameter is the easiest tree attribute to measure. Zianis et al. (2005) list only 30.3% out of the 607 equations that are based on both height and dbh. The inclusion of tree height as a variable in allometric equations was studied by various authors (e.g. Xiao and Ceulemans 2004; Cienciala et al. 2006; Bronisz and Zasada 2016). According to Marklund (1987), Socha and Wężyk (2007), or Ruiz-Peinado et al. (2011), inclusion of tree height improves aboveground biomass estimates. On the contrary, Jenkins et al. (2003) as well as Peichl and Arain (2006) found that height is an undesirable variable due to the difficulties in accurate measurements and only marginal improvements of dbh-based equations. In case of models for small trees, application of tree height gives better biomass estimates than using only diameter at ground level, as reported by Dutca et al. (2010). However, Pajtík et al. (2008) found that stem base diameter offers slightly more precise estimates of trees biomass than height. In our study, after the inclusion of height as an independent variable in the allometric models, we observed a considerable increase in the overall model accuracy for both biomass components and total aboveground biomass.
The calculation of the biomass of trees that have not reached the height of 1.3 m yet is one of the substantial issues in the estimation of biomass stocks in very young stands, especially when dbh-based allometric equations are used in general. One solution could be the addition of the intercept to the model for large trees (i.e. dbh-based one). This eliminates the model bias created by forcing biomass to be zero when trees are 1.3 meters tall. However, the inclusion of an intercept in the model for large trees and its application for trees shorter than 1.3 m results in a constant biomass value for these trees. This, in turn, gives biased estimation of the total biomass of the stand. More logical and less biased results are obtained when the stem base diameter (d0) is applied in the allometric equations (Pajtík et al. 2008; Dutca et al. 2010). However, as indicated by our results, the extension of this parameter usage for trees that already have dbh results in a decrease of the model accuracy.
An important aspect of our study is the consideration of various tree components in biomass calculations. The principal difference between the presented analysis and formulas developed for silver birch in the Baltic States and Scandinavia by Johansson (1999), Repola (2008), Varik et al. (2009), Uri et al. (2012), Liepiņš (2013), and Smith et al. (2014) is based on the fact that we used a different approach to equation construction than these authors. The applied seemingly unrelated regression method assures the logical condition that the sum of biomass of various components is equal to the total tree biomass. Such an approach has an obvious advantage for the practical application of the elaborated models (Parresol 1999).
Lack of local biomass models forces practitioners to use the equations adopted from the literature. Such a solution can be justified and methodologically proper; however, it may result in significant bias of the obtained estimates (Wang et al. 2002; Ochał et. al 2014). Literature-taken allometric models should be carefully used, especially outside the range of the parameters used for their elaboration. The majority of the analyzed ‘not-local’ simplified models overestimate total aboveground biomass for thin (dbh < 4 cm) as well as for thick (dbh > 8 cm) trees, while underestimate this parameter for medium individuals (dbh 4–8 cm). The equation from Johansson (1999) for all trees yields higher biomass values than our simplified model. On the other hand, the high consistency of total aboveground biomass estimates obtained with the expanded models seems to support the concept of inclusion of height as the additional parameter in biomass equations, as it increases a chance of reducing bias resulting from the use of equations designed for different growing conditions.
It might also be important to consider choosing equations developed for the environmental conditions most similar to those of the respective study. The best fitting simplified model is based on the equations developed for the stand growing on former farmland, while the worst fitting one is based on data for forest stands (Uri et al. 2012).
6 Conclusions
Biomass models based on diameter and height (expanded models) were characterized based on better fit to data than models based exclusively on diameter (simplified ones), especially for the variables total aboveground and stem biomass. Application of the diameter at ground level in the allometric equations should be restricted to estimation of biomass of trees shorter than 1.3 m as for the larger trees, diameter at breast height is a better biomass predictor in both simplified and expanded models. Silver birch biomass estimates derived with models from the neighboring countries are generally consistent with those determined with equations presented in this study, especially for the expanded models and as far as tree parameters such as dbh and/or height are similar to those used in model parametrization.
Acknowledgements
The research presented in this paper was done in the frame of the research grant N N305 400238 ”Ecological consequences of the silver birch (Betula pendula Roth.) secondary succession on abandoned farmlands in central Poland” funded by the Polish National Science Center.
References
Adegbidi H.G., Jokela E.J., Comerford N.B., Barros N.F. (2002). Biomass development for intensively managed loblolly pine plantations growing on Spodosols in the southeastern USA. Forest Ecology and Management 167(1–3): 91–102. http://dx.doi.org/10.1016/S0378-1127(01)00691-0.
Alves L.F., Vieira S.A., Scaranello M.A., Camargo P.B., Santos F.A.M., Joly C.A., Martinelli L.A. (2010). Forest structure and live aboveground biomass variation along an elevational gradient of tropical Atlantic moist forest (Brazil). Forest Ecology and Management 260(5): 679–691. http://dx.doi.org/10.1016/j.foreco.2010.05.023.
Balboa-Murias M.Á., Rodríguez-Soalleiro R., Merino A., Álvarez-González J.G. (2006). Temporal variations and distribution of carbon stocks in aboveground biomass of radiata pine and maritime pine pure stands under different silvicultural alternatives. Forest Ecology and Management. 237(1–3): 29–38. http://dx.doi.org/ 10.1016/j.foreco.2006.09.024.
Bates D., Watts D.G. (2007). Nonlinear regression analysis and its applications. Wiley. ISBN 978-0-470-13900-4.
Belsley D.A., Kuh E., Welsch R.E. (1980). Regression diagnostics: identifying influential data and sources of collinearity. John Wiley and Sons Incorporation, Hoboken, New York, USA. http://doi.wiley.com/10.1002/0471725153.
Bi H., Long Y., Turner J., Lei Y., Snowdon P., Li Y., Harper R., Zerihun A., Ximenes F. (2010). Additive prediction of aboveground biomass for Pinus radiata (D. Don) plantations. Forest Ecology and Management 259(12): 2301–2314. http://dx.doi.org/10.1016/j.foreco.2010.03.003.
Bijak Sz., Zasada M., Bronisz A., Bronisz K., Czajkowski M., Ludwisiak Ł., Tomusiak R., Wojtan R. (2013). Estimating coarse roots biomass in young silver birch stands on post-agricultural lands in central Poland. Silva Fennica 47(2): 1–14. http://dx.doi.org/10.14214/sf.963.
Birdsey R.A. (1992). Carbon storage and accumulation in United States forest ecosystems. General technical no. WO-59. Forest Service, United States. 51 p.
Bronisz K., Zasada M. (2016). Uproszczone wzory empiryczne do określania suchej biomasy nadziemnej części drzew i ich komponentów dla sosny zwyczajnej. [Simplified empirical formulas to determine the dry biomass of aboveground components of trees for Scots pine]. Sylwan 160(4): 277–283. [In Polish].
Brown S., Schroeder P., Kern J.S. (1999). Spatial distribution of biomass in forests of the eastern USA. Forest Ecology and Management 123(1): 81–90. http://dx.doi.org/10.1016/S0378-1127(99)00017-1.
Carvalho J.P., Parresol B.R. (2003). Additivity in tree biomass components of Pyrenean oak (Quercus pyrenaica Willd.). Forest Ecology and Management 179(1–3): 269–276. http://dx.doi.org/10.1016/S0378-1127(02)00549-2.
Chiyenda S.S., Kozak A. (1984). Additivity of component biomass regression equations when the underlying model is linear. Canadian Journal of Forest Research 14(3): 441–446. http://dx.doi.org/10.1139/x84-078.
Cienciala E., Černý M., Tatarinov F., Apltauer J., Exnerová Z. (2006). Biomass functions applicable to Scots pine. Trees 20(4): 483–495. http://dx.doi.org/10.1007/s00468-006-0064-4.
Cotillas M., Espelta J.M., Sánchez-Costa E., Sabaté S. (2016). Aboveground and belowground biomass allocation patterns in two Mediterranean oaks with contrasting leaf habit: an insight into carbon stock in young oak coppices. European Journal of Forest Research 135(2): 243–252. http://dx.doi.org/ 10.1007/s10342-015-0932-9.
Cunia T., Briggs R.D. (1984). Forcing additivity of biomass tables – some empirical results. Canadian Journal of Forest Research 15(1): 23–28. http://dx.doi.org/10.1139/x85-006.
Daugaviete M., Gaitnieks T., Kļaviņa D., Teliševa G. (2008). Oglekļa akumulācija virszemes un sakņu biomasā priedes, egles un bērza stādījumos lauksaimniecības zemēs. [Carbon accumulation in the above-ground and root biomass of pine, birch and spruce cultivated in agricultural soils). Mežzinātne 18: 35–52. [In Latvian].
Detwiler R.P., Hall C.A. (1988). Tropical forests and the global carbon cycle. Science 239(4835): 42–47. http://dx.doi.org/10.1126/science.239.4835.42.
Dutca I., Abrudan I.V., Stancioiu P.T., Blujdea V. (2010). Biomass convertion and expansion factors for young Norway spruce (Picea abies (L.) Karst.) trees planted on non-forest lands in Eastern Carpathians. Notulae Botanicae Horti Agrobotanici Cluj-Napoca 38: 286–292.
Elowson S. (1996). Birch-a highproducing species. In: Perttu K., Koppel A. (eds.). Short rotation willow coppice for renewable energy and improved environment. Uppsala. p. 107.
European Council conclusions (No. EUCO 169/14). (2014). European Council, Brussel.
Fahey T.J., Woodbury P.B., Battles J.J., Goodale C.L., Hamburg S.P., Ollinger S.V., Woodall C.W. (2009). Forest carbon storage: ecology, management, and policy. Frontiers in Ecology and the Environment 8(5): 245–252. http://dx.doi.org/10.1890/080169.
Ferm A. (1993). Birch production and utilization for energy. Biomass and Bioenergy 4(6): 391–404. http://dx.doi.org/10.1016/0961-9534(93)90061-8.
González-García S., Mola-Yudego B., Murphy R.J. (2013). Life cycle assessment of potential energy uses for short rotation willow biomass in Sweden. The International Journal of Life Cycle Assessment 18(4): 783–795. http://dx.doi.org/10.1007/s11367-012-0536-2.
Jagodziński A.M., Kałucka I., Horodecki P., Oleksyn J. (2014). Aboveground biomass allocation and accumulation in a chronosequence of young Pinus sylvestris stands growing on a lignite mine spoil heap. Dendrobiology 72: 139–150. http://dx.doi.org/10.12657/denbio.072.012.
Jenkins J.C., Chojnacky D.C., Heath L.S., Birdsey R.A. (2003). National-scale biomass estimators for United States tree species. Forest Science 49: 12–35.
Johansson T. (1999). Biomass equations for determining fractions of pendula and pubescent birches growing on abandoned farmland and some practical implications. Biomass and Bioenergy 16(3): 223–238. http://dx.doi.org/10.1016/S0961-9534(98)00075-0.
Johansson T. (2007). Biomass production and allometric above- and below-ground relations for young birch stands planted at four spacings on abandoned farmland. Forestry 80(1): 41–52. http://dx.doi.org/10.1093/forestry/cpl049.
Karlsson A., Albrektson A., Forsgren A., Svensson L. (1998). An analysis of successful natural regeneration of downy and silver birch on abandoned farmland in Sweden. Silva Fennica 32(3): 229–240. http://dx.doi.org/10.14214/sf.683.
Kozak A. (1970). Methods for ensuring additivity of biomass components by regression analysis. The Forestry Chronicle 46(5): 402–405. http://dx.doi.org/10.5558/tfc46402-5.
Krawczyk R. (2015). Afforestation and secondary succession. Forest Research Papers 75(4): 423–427. http://dx.doi.org/10.2478/frp-2014-0039.
Kuznetsova T., Lukjanova A., Mandre M., Lõhmus K. (2011). Aboveground biomass and nutrient accumulation dynamics in young black alder, silver birch and Scots pine plantations on reclaimed oil shale mining areas in Estonia. Forest Ecology and Management 262(2): 56–64. http://dx.doi.org/10.1016/j.foreco.2010.09.030.
Liepiņš K. (2013). Modelis koksnes biomasas aprēķināšanai bērza jaunaudzēs. http://www.silava.lv/23/section.aspx/View/127. [In Latvian].
Lupi C., Larocque G., DesRochers A., Labrecque M., Mosseler A., Major J., Beaulieu J., Tremblay F., Gordon A.M., Thomas B.R., Vézina A., Bouafif H., Cormier D., Sidders D., Krygier R., Thevathasan N., Riopel M., Ferland-Raymond B. (2015). Evaluating sampling designs and deriving biomass equations for young plantations of poplar and willow clones. Biomass and Bioenergy 83: 196–205. http://dx.doi.org/10.1016/j.biombioe.2015.09.019.
Mälkönen E. (1977). Annual primary production and nutrient cycle in a birch stand. Communicationes Instituti Forestalis Fenniae 91(5). 35 p.
Marklund L.G. (1987). Biomass functions for Norway spruce (Picea abies (L.)) in Sweden. Department of Forest Survey, Swedish University of Agricultural Sciences. Umeå, Sweden.
Marklund L.G. (1988). Biomassafunktioner för tall, gran och björk i Sverige. [Biomass functions for pine, spruce and birch in Sweden]. Department of Forest Survey, Swedish University of Agricultural Sciences. Umeå, Sweden. [In Swedish].
Martyn D. (2000). Klimaty kuli ziemskiej. [Climates of the Earth]. PWN, Warsaw. [In Polish].
Muukkonen P. (2007). Generalized allometric volume and biomass equations for some tree species in Europe. European Journal of Forest Research 126(2): 157–166. http://dx.doi.org/10.1007/s10342-007-0168-4.
Ochał W., Socha J., Grabczyński S. (2014). Dokładność wzorów empirycznych służących do określania biomasy nadziemnych komponentów drzew olszy czarnej (Alnus glutinosa (L.) Gaertn.). [Accuracy of empirical formulas for determining aboveground biomass of black alder (Alnus glutinosa (L.) Gaertn.)]. Sylwan 158(6): 431–442. [In Polish].
Oleksyn J., Reich P.B., Chalupka W., Tjoelker M.G. (1999). Differential above-and below-ground biomass accumulation of European Pinus sylvestris populations in a 12-year-old provenance experiment. Scandinavian Journal of Forest Research 14(1): 7–17. http://dx.doi.org/10.1080/02827589908540804.
Pajtík J., Konôpka B., Lukac M. (2008). Biomass functions and expansion factors in young Norway spruce (Picea abies [L.] Karst) trees. Forest Ecology and Management 256(5): 1096–1103. http://dx.doi.org/10.1016/j.foreco.2008.06.013.
Pajtík J., Konôpka B., Lukac M. (2011). Individual biomass factors for beech, oak and pine in Slovakia: a comparative study in young naturally regenerated stands. Trees 25(2): 277–288. http://dx.doi.org/10.1007/s00468-010-0504-z.
Parresol B.R. (1999). Assessing tree and stand biomass: a review with examples and critical comparisons. Forest science 45: 573–593.
Peichl M., Arain M.A. (2006). Above- and belowground ecosystem biomass and carbon pools in an age-sequence of temperate pine plantation forests. Agricultural and Forest Meteorology 140: 51–63. http://dx.doi.org/10.1016/j.agrformet.2006.08.004.
R Development Core Team (2008). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
Repola J. (2008). Biomass equations for birch in Finland. Silva Fennica 42(4): 605–624. http://dx.doi.org/10.14214/sf.236.
Ribeiro S.C., Fehrmann L., Soares C.P.B., Jacovine L.A.G., Kleinn C., de Oliveira Gaspar R. (2011). Above- and belowground biomass in a Brazilian Cerrado. Forest Ecology and Management 262(1): 491–499. http://dx.doi.org/10.1016/j.foreco.2011.04.017.
Rittenhouse C.D., Rissman A.R. (2012). Forest cover, carbon sequestration, and wildlife habitat: policy review and modeling of tradeoffs among land-use change scenarios. Environmental Science and Policy 21: 94–105. http://dx.doi.org/10.1016/j.envsci.2012.04.006.
RStudio Team (2015). RStudio: integrated development for R. RStudio, Inc., Boston, MA URL http://www.rstudio.com/.
Ruiz-Peinado R., del Rio M., Montero G. (2011). New models for estimating the carbon sink capacity of Spanish softwood species. Forest Systems 20(1): 176–188. http://dx.doi.org/10.5424/fs/2011201-11643.
Samuelsson R., Burvall J., Jirjis R. (2006). Comparison of different methods for the determination of moisture content in biomass. Biomass and Bioenergy 30(11): 929–934. http://dx.doi.org/10.1016/j.biombioe.2006.06.004.
SAS 9.1.3 Help and Documentation (2002). SAS Institute Incorporation. Cary, North Carolina.
Skovsgaard J.P., Nord-Larsen T. (2012). Biomass, basic density and biomass expansion factor functions for European beech (Fagus sylvatica L.) in Denmark. European Journal of Forest Research 131(4): 1035–1053. http://dx.doi.org/10.1007/s10342-011-0575-4.
Smith A., Granhus A., Astrup R., Bollandsås O.M., Petersson H. (2014). Functions for estimating aboveground biomass of birch in Norway. Scandinavian Journal of Forest Research 29(6): 565–578. http://dx.doi.org/10.1080/02827581.2014.951389.
Smith A., Granhus A., Astrup R. (2016). Functions for estimating belowground and whole tree biomass of birch in Norway. Scandinavian Journal of Forest Research, January 2016. 15 p. http://dx.doi.org/10.1080/02827581.2016.1141232.
Snowdon P., Raison J., Keith H., Ritson P., Grierson P., Adams M.A., Montagu K., Hui-quan B., Burrows W., Eamus D. (2002). Protocol for sampling tree and stand biomass. National carbon accounting system technical report no. 31. Australian Greenhouse Office, Australia.
Socha J., Wężyk P. (2004). Empirical formulae to assess the biomass of the above-ground part of pine trees. Electronic Journal of Polish Agricultural Universities, Forestry 7. http://www.ejpau.media.pl/volume7/issue2/forestry/art-04.html.
Socha J., Wężyk P. (2007). Allometric equations for estimating the foliage biomass of Scots pine. European Journal of Forest Research 126(2): 263–270. http://dx.doi.org/10.1007/s10342-006-0144-4.
Szwagrzyk J. (2004). Sukcesja leśna na gruntach porolnych; stan obecny, prognozy i wątpliwości. [Forest succession on abandoned farmland; current estimates, forecasts and uncertainties]. Sylwan 148(4): 53–59. [In Polish].
Tahvanainen T., Forss E. (2008). Individual tree models for the crown biomass distribution of Scots pine, Norway spruce and birch in Finland. Forest Ecology and Management 255(3–4): 455–467. http://dx.doi.org/10.1016/j.foreco.2007.09.035.
Teobaldelli M., Somogyi Z., Migliavacca M., Usoltsev V.A. (2009). Generalized functions of biomass expansion factors for conifers and broadleaved by stand age, growing stock and site index. Forest Ecology and Management 257(3): 1004–1013. http://dx.doi.org/10.1016/j.foreco.2008.11.002.
Ter-Mikaelian M.T., Korzukhin M.D. (1997). Biomass equations for sixty-five North American tree species. Forest Ecology and Management 97(1): 1–24. http://dx.doi.org/10.1016/S0378-1127(97)00019-4.
Uri V., Vares A., Tullus H., Kanal A. (2007). Above-ground biomass production and nutrient accumulation in young stands of silver birch on abandoned agricultural land. Biomass and Bioenergy 31(4): 195–204. http://dx.doi.org/10.1016/j.biombioe.2006.08.003.
Uri V., Varik M., Aosaar J., Kanal A., Kukumägi M., Lõhmus K. (2012). Biomass production and carbon sequestration in a fertile silver birch (Betula pendula Roth) forest chronosequence. Forest Ecology and Management 267(1): 117–126. http://dx.doi.org/10.1016/j.foreco.2011.11.033.
van Kooten G.C., Eagle A.J., Manley J., Smolak T. (2004). How costly are carbon offsets? A meta-analysis of carbon forest sinks. Environmental Science and Policy 7(4): 239–251. http://dx.doi.org/10.1016/j.envsci.2004.05.006.
Van Tuyl S., Law B.E., Turner D.P., Gitelman A.I. (2005). Variability in net primary production and carbon storage in biomass across Oregon forests-an assessment integrating data from forest inventories, intensive sites, and remote sensing. Forest Ecology and Management 209(3): 273–291. http://dx.doi.org/10.1016/j.foreco.2005.02.002.
Varik M., Aosaar J., Uri V. (2009). Biomass production in silver birch stands in Oxalis site type. Forestry Studies/Metsanduslikud Uurimused 51: 5–16. http://dx.doi.org/10.2478/v10132-011-0073-y.
Wang J.R., Zhong A.L., Kimmins J.P. (2002). Biomass estimation errors associated with the use of published regression equations of paper birch and trembling aspen. Northern Journal of Applied Forestry 19(3): 128–136.
Wickham H. (2009). Getting started with qplot. In: ggplot2. Springer. p. 9–26. http://dx.doi.org/10.1007/978-0-387-98141-3_2.
Xiao C.-W., Ceulemans R. (2004). Allometric relationships for below- and aboveground biomass of young Scots pines. Forest Ecology and Management 203(1–3): 177–186. http://dx.doi.org/10.1016/j.foreco.2004.07.062.
Zając S., Gil W. (2003). Zalesienia w Europie – doświadczenia i zamierzenia. [Afforestation in Europe-experiences and prospects]. Forest Research Institute, Warsaw. ISBN 83-87647-33-0. [In Polish].
Zasada M., Bronisz K., Bijak Sz., Wojtan R., Tomusiak R., Dudek A., Michalak K., Wróblewski L. (2008). Wzory empiryczne do określania suchej biomasy nadziemnej części drzew i ich komponentów. [Empirical formulae for determination of the dry biomass of aboveground parts of the tree]. Sylwan 152(3): 27–39. [In Polish].
Zasada M., Bronisz K., Bijak Sz., Dudek A., Bruchwald A., Wojtan R., Tomusiak R., Bronisz A., Wróblewski L., Michalak K. (2009). Effect of the cutting age and thinning intensity on biomass and carbon sequestration – the Gubin Forest District case study. Folia Forestalia Polonica, series A 51(2): 138–144.
Zasada M., Bijak Sz., Bronisz K., Bronisz A., Gawęda T. (2014). Biomass dynamics in young silver birch stands on post-agricultural lands in central Poland. Drewno 57(192): 29–40. http://dx.doi.org/10.12841/wood.1644-3985.S07.02.
Zellner A. (1962). An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. Journal of American Statistical Association 57(298): 348–368. http://dx.doi.org/10.1080/01621459.1962.10480664.
Zianis D., Muukkonen P., Mäkipää R., Mencuccini M. (2005). Biomass and stem volume equations for tree species in Europe. Silva Fennica Monographs 4. 63 p.
Total of 76 references.

