Log yard logistics
Huka M. A., Gronalt M. (2018). Log yard logistics. Silva Fennica vol. 52 no. 4 article id 7760. https://doi.org/10.14214/sf.7760
Highlights
- Characteristics of log yard logistics
- Classification into tactical structural and operational problems in the wood industry
- Different solution methods such as optimisation, heuristics and simulations and their possible application within the log yard with an overview of existing literature which includes several different case studies with varying emphases, problem analysis and solution methods.
Abstract
For sawmills, paper mills, particleboard, oriented strand board (OSB), fiberboard and other wood production factories, the log yard is the first step, where raw materials are sorted and stored before production begins. Due to the size of these production sites great potential exists for the optimisation of internal logistics. In this paper the different planning problems of the log yard are introduced and existing literature examined. Beginning with the tactical problems of structure, such as assessing material flow, planning facility layout and assigning storage areas, it continues with operational problems such as vehicle movement planning within the log yard, empty trip minimisation and the seasonality of raw material availability. Data derived from this study reveals a variety of possible solution methods, the applicability of which depends on the precise nature of the log yard operations. Additionally, several real life examples are provided which illustrate the potential for operational improvement.
Keywords
log yard;
tactical structural and operational problems;
material flow;
facility layout planning;
storage assignment;
vehicle movement;
seasonality
-
Huka,
University of Natural Resources and Life Sciences, Institute of Production and Logistics, Feistmantelstraße 4, 1180 Vienna, Austria
E-mail
maria.huka@boku.ac.at

- Gronalt, University of Natural Resources and Life Sciences, Institute of Production and Logistics, Feistmantelstraße 4, 1180 Vienna, Austria E-mail manfred.gronalt@boku.ac.at
Received 28 June 2017 Accepted 6 September 2018 Published 12 September 2018
Views 97019
Available at https://doi.org/10.14214/sf.7760 | Download PDF

List of symbols
| OSB | Oriented strand board |
| GDP | Gross domestic product |
| m3 | Cubic meter |
| L | Set of locations |
| Djk | Distance of locations j and k (equivalent to Dij) |
| Ahi | Number of transportation runs between location h and i (equivalent to Aij) |
| xhj | Number of trips between location h and j (equivalent to xik and xij) |
| λij | Transportation matrix for locations i and j |
| Hisource | Source characteristics of location i |
| Hjsink | Sink characteristics of location j (equivalent to Hisink) |
| Si | Supply of vehicles at location i |
| Ni | Demand for vehicles at location i (equivalent to Nj) |
| δij | Number of empty trips from location i to j |
1 Introduction
As analysed in detail by Lebedys and Li (2014), the contribution of forestry to national gross domestic product (GDP) is, for many countries, slightly declining. Despite this the industry remains a very important sector of many economies and as such provides significant opportunities for process improvement and optimisation. Since the marketing of this sector is globally oriented, low costs of production and transportation ensure its competitiveness whilst providing high revenues. This has been previously described by Rönnqvist (2003) who illustrates the nature of the forest-based industries and describes and summarises the variety of planning problems. The work summarises the problems which arise in the strategic planning for forest management, where the time scale can be hundreds of years, the tactical planning of harvesting in a time period of a few months to a year and includes short term operational planning such as transportation, routing and production planning.
Another review paper analysing the potential for optimisation in forestry, Rahman et al. (2014a) structure the existing research work according to the optimisation or simulation techniques used. Their paper introduces linear and integer programming over artificial intelligence-based methods and simulations however little research is provided on the improvement of the logistical operations within a production site’s log yard.
In the currently existing literature the main focus of forestry research is on: production planning (Kazemi Zanjani et al. 2010; Maturana et al. 2010; Vergara et al. 2015; Huka and Gronalt 2017), supply chain management (Singer and Donoso 2007; D’Amours et al. 2008; Santa-Eulalia et al. 2012; Bouchard et al. 2017) and value chain optimisation (Audy et al. 2014; Gendron et al. 2016) with few papers addressing the potential of logistic optimisation within the log yard. The main contribution of this paper is to gather the existing literature on optimising the log yard logistics and divide the problems arising into those of tactical structural and operational planning. Additionally, newly relevant planning problems within different areas of processes are identified and solutions suggested. The paper concludes with selected case studies, where methods previously described in the paper are applied.
2 Log yard logistics analysis
2.1 Definition of a log yard
A good overview of different types of log yards can be found in the report by Dramm et al. (2002) where concepts and advantages applicable to the forest industry in the United States are discussed and analysed. Gronalt and Rauch (2018) apply a discrete event simulation to examine the prevailing wood railroad terminal layout configurations in order to show systems bottlenecks and reveal potential improvements. In this paper, however, the focus is on log yards integrated into forestry production sites rather than the external yards used for gathering and sorting the raw material. The primary wood industry, sawmills, board industries and power plants handle raw material which is both heavy and bulky. This, combined with the complexity of the material, with its varying dimensions of length and diameter, different stacking requirements, variety of species plus the nature of the output (which is not only logs but includes sawmill by-products such as wood chips, sawdust, bark, slabs and recycled wood) necessitates log yards of considerable size. Size also aids somewhat in stabilizing the production process since availability and price fluctuation could otherwise disrupt the production planning process as can the internal distribution grading of wood, a process which is undertaken after initial processing. Additionally, apart from log yard size, the high cost of capital equipment has to be taken into consideration. Fig. 1 shows a schematic diagram of a theoretical log yard serving a combination of sawmill, various board productions, a paper mill and a power plant and illustrates the different ways raw material can be handled and processed. The raw timber can be delivered as whole stems or already cut-to-length, sorted by species and dimensions or in mixed batches which may or may not have been debarked. Furthermore, the consistency of recycled wood varies from log yard to log yard. It can either be chipped before arriving at the log yard or later but, in most cases, it needs to be sorted and inspected to identify the quality and consistency.
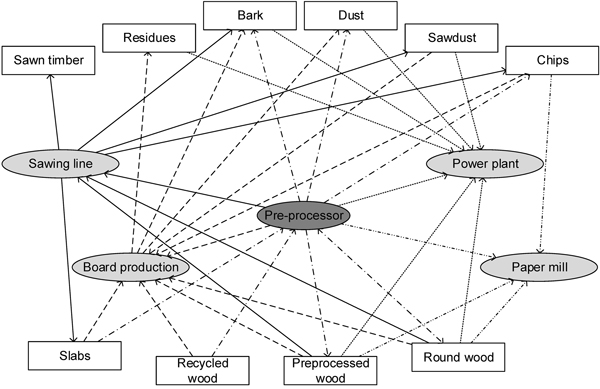
Fig. 1. Schematic log yard diagram of a super wood factory where a sawmill is combined with board production, paper mill and a power plant. The pre-processor is an additional possible step before production which can be debarking, bucking, chipping or particle preparation.
The optimisation of log yard logistics is complicated by the variety of input materials, the handling technologies available, the vehicle types and the complexity of the material flow, which is itself dependent on the production process employed. Clearly then, given the nature of the globalized market, structured layout development, cost-efficient material handling and warehousing are becoming increasingly important elements of efficient log yard operations. Though it can be investigated either as sub-problems of the whole or sequentially, as individual problems, little research has been conducted. Table 1 shows the different subject areas of existing literature which have been investigated and the solution method the respective authors used to solve the specific problem.
| Table 1. Papers on log yard logistics with different subject areas and solution methods. | ||
| Authors | Subject area | Used method |
| Baesler et al. (2002) | Loader scheduling | Simulation optimisation; Genetic algorithm heuristic |
| Beaudoin et al. (2012) | Material flow analysis; Loader scheduling and duty assignment | Discrete event simulation |
| Rathke et al. (2013) | Facility layout planning; Storage assignment | Mixed integer programming model; Heuristic |
| Rahman et al. (2014b) | Storage assignment; Seasonality | Discrete event simulation; Metaheuristic |
| Robichaud et al. (2014) | Material flow analysis; Facility layout planning; Loader scheduling; Seasonality | Discrete event simulation |
| Silver and Zufferey (2005) | Inventory management; Seasonality | Heuristic; Tabu Search; Simulation |
| Shaik et al. (2012) | Loader scheduling | Multi-agent based simulation |
| Yujie and Fang (2009) | Material flow analysis; Facility layout planning | Relationship chart; Correlation and closeness table |
2.2 Special features on the log yard
The log yard is usually outdoors and has to cope with a variety of weather conditions. Special infrastructure needs to be provided such as light towers that divide the storage area and sprinklers for quality issues of the logs. As mentioned before, a large storage space is needed for the volume of processed raw material. The different qualities, species and sometimes varying origins and certifications with the same dimensions can lead to even more assortments and space requirements as can the different geometries, bulk and piece goods, which require different vehicles in the log yard. The material flow can further be complicated by different delivery methods such as truck, train or ship and several possible material charges, different sawing or production lines or pre-processing. Moreover, the ground surface, concrete, asphalt or gravel, determines both the weight per area which can be stored there and the type of the stored material. In addition, a strict first-in-first-out policy needs to be pursued to prevent quality losses through biological or chemical degradation. This leads to detailed considerations of the placement of storage areas and their accessibility. Also, dealing with a natural resource entails seasonal variation in supply. Several safety regulations have to be considered on the log yard as well. The minimal distance of buildings to storage areas has to be kept and piles of chips and sawdust have to be mixed and rearranged to prevent fire due to biological deterioration and the resulting heat build-up. The potential fire risk limits the overall size of storage areas. The safety of pedestrians has to be considered and special footways have to be planned to prevent collisions with the heavy machinery. In order to clarify the different challenges of log yard logistics specific management requirements are worked out at the beginning of this paper. Clearly, the focus of log yard logistics is always on material movement and storage.
2.3 Log yard operations and management support
The whole production site and its process benefit from a better organized log yard. The first step then is to determine the goal of the analysis and to examine relevant improvement options. The next step is to select the appropriate evaluation method for each option. For some problems simulation is better suited than a mathematical model. All the conflicting goals have to be considered and choices made such as minimising distances travelled versus storage space, planning reserve capacities versus just-in-time storage or balanced work share versus minimisation of vehicles versus maintenance planning. Furthermore, potential investment decisions can be investigated or different policies within the log yard can be studied and established. In a further step, the problem of log yard logistics can be embedded in the productivity of the whole supply chain. The next step of the analysis is to gather the underlying data, examine the yard dimensions and its layout, compute the distances within the yard and investigate the boundary conditions. Moreover, the storage needs to be analysed with reference to the number of assortments, the space each element requires, their maximum storage heights, storage requirements, raw material geometries and the driveways necessary. Furthermore, the different vehicles, used or potential, together with their specific properties and applications are investigated. These basic elements of layout, storage and vehicle data for the analysis of the log yard logistic problem are described in Table 2.
| Table 2. Basic elements: data, storage, transport (vehicles and loaders). | ||
| Data | • Volume | • Weight |
| • Yard dimensions | • Yard layout | |
| • Distances | • Location of fixed items | |
| • Seasonality in data | • Boundary conditions | |
| • Number of assortments | ||
| Storage | • Needed space | • Geometries |
| • Storage requirements | • Driveways | |
| • Maximum storage heights | ||
| Vehicles | • Vehicle types | • Duties |
| • Transportation fleet variety | • Capacity per trip | |
| • Multimodality | • Shift models | |
| • Schedule | • Non-profitable duties | |
| • Loading and unloading | • Technical details | |
| • Costs | ||
In the last step the suitable material and methods for improving log yard operations need to be determined. The appropriate or preferred solution method, dynamic versus static, exact versus heuristic, simulation versus optimisation or integrated into an existing IT-solution, needs to be chosen (Table 3). The following section divides the planning problem of log yard logistics into three main smaller sub-problems which arise when planning or handling a log yard.
| Table 3. Planning problems. | ||
| Problems | Applications | |
| Tactical structural planning | • Material flow overview • Facility layout planning • Storage assignment | • New facilities planning ∘ Placement of grading and measuring stations ∘ Location of machines • Evaluation of log yards ∘ In/dependent storage assignment |
| Operational planning | • Material movement • Empty trips • Seasonality and raw material supply | • Operations and IT support ∘ IT-systems integration • Loader control system ∘ Loaded and empty runs ∘ Routing and dispatch of loaders • Frequency and re-planning ∘ One time setup planning ∘ Automatic re-planning for seasonality |
3 Tactical structural problems
3.1 Material flow overview
For facility layout planning a good knowledge of the existing material flow and space restrictions is crucial. The first step to expand or plan a layout for a log yard is to analyse the existing material flow within it and extract valid data based on the different assortments. Further, their final destination within the log yard, namely the processing machine, has to be specified. In addition, the number of the assortments needs to be estimated. Material flow can be analysed with qualitative and quantitative measurements. Qualitative measures describe restrictions or suggestions for the placement of assortments or production segments in relation to each other, whereas quantitative measures are given in amount per time such as litre per second or tons per shift. Muther (1973) introduces closeness relationship values for the qualitative measurement of material flow. These values can be summarised in a relationship chart and together with the reasons for the closeness values illustrated in Tompkins et al. (2010) they indicate boundary placement restrictions for the different assortments. This veers toward a possible layout solution of the facility.
Yujie and Fang (2009) use this technique to determine a good layout for a log yard with a total area of 19.5 hectares in Heilongjiang Province with a total annual timber flow of 85 375 m³. This log yard is a combined facility used by eight forest farms located separately outside of the factories. Despite this, the proposed method for arranging assortments is appropriate. After analysing the basic elements of the technological process within the log yard the authors divide it into operation areas and develop a correlation and closeness table for the logistics and non-logistics. As a next step the authors determine the extent of closeness of the relationship between the operating regions and draw the related location map of the operating area. Next, they identify the actual area of each operating area and the material flow pattern. With this information they establish the actual layout of the log yard.
Besides a directed graph and a from-to-chart another possible tool to show the quantitative material flow is the Sankey diagram which is based on Minard (1870) and further established by Sankey (1898). For details on the history of the Sankey diagram see Schmidt (2008). A Sankey diagram is a specific type of flow diagram where the width of the arrows proportionally shows the flow quantity and is more advantageous compared to a simpler directed graph and from-to chart. The Sankey diagram is suited to find inefficiencies and reveal saving potentials. Moreover, it is possible to map value flows with this kind of diagram. Knowing the material flow the required log yard capacities can be roughly estimated and the actual layout can be planned. The advantages of the use of a Sankey diagram are shown in a case study in Section 5.3.
3.2 Facility layout planning
Facility layout planning is a well-known concept introduced by Koopmans and Beckmann (1957) who propose a model to the problem of placing plants with material flow in between. It can be implemented in different levels of detail such as arranging buildings in a factory or positioning tools on a workbench. Methods for facility layout planning may act on the design of production lines and the arrangement of material feeding as well as for providing room for the workers to complete their tasks properly and may also be applied for the whole plant. Kusiak and Heragu (1987) prepare a survey and comparison of different solution methods and heuristics for the facility layout problem. Furthermore, Drira et al. (2007) give an overview of the different layout representations, the formulations of layout problems and their respective solution approaches however there are not many applications in the forestry production. Balakrishnan et al. (2003) for example propose an efficient but also user-friendly heuristic approach to solve the static facility layout problem with unequal department sizes which can be used on the log yard. Their method uses two effective algorithms, simulated annealing and genetic algorithms, to generate a heuristic layout solution. Furthermore, Abotaleb et al. (2016) describe a new approach to the facility layout planning of construction site layout problems based on genetic algorithms which can handle non-rectilinear shapes and mimics dynamic behaviour of geometries of site facilities. This means the facilities are modelled using a geometric shape, such as offset planar curves, dynamic freeforms or dynamic rectangles and their dimension and form can change in each run of the algorithm. Moreover, the model provides different proximity measures and therefore allows movement between the facilities including passageways and access roads. According to Singh and Sharma (2006) the facility layout problems can be classified into static and dynamic problems and solved with different solution approaches such as quadratic integer programming, mixed integer programming or by the use of graph theory. The facility layout problem is modelled and solved to find an efficient layout for facilities on a site. Tompkins et al. (2010) describe the facility layout planning process as a holistic fundamental component of the supply chain. Due to contrary objectives of the facility planning the main goal of the layout planning has to be identified and potential optimisation losses of contrary objectives have to be considered. The placement of the facilities within the plant area has a significant impact on manufacturing costs, work in process, lead times and productivity. A good placement therefore contributes to the overall efficiency of operations and can reduce up to 50 percent, the total operating expenses. Page (1991) reports that, on average, 40 percent of a company’s sales come from new products. However, the change in product mix leads to a modification of the production flow and thus affects the layout. Gupta and Seifoddini (1990) state that many companies undergo major reorganization of the production facilities every two years. In forest-based industries it can be observed that advances in production technology or a change in material flows are seldom directly addressed in newly optimised layouts. On the other hand, transportation distances in production facilities of forest-based industries are usually very large and cause high movement costs. Decision support is needed to show how to deal with technology changes in production and how to efficiently incorporate new material flows in a facility. Consequently, facility layout planning is a continuous improvement process because it must adapt to new products, market changes and alternative production technologies (Fig. 2).
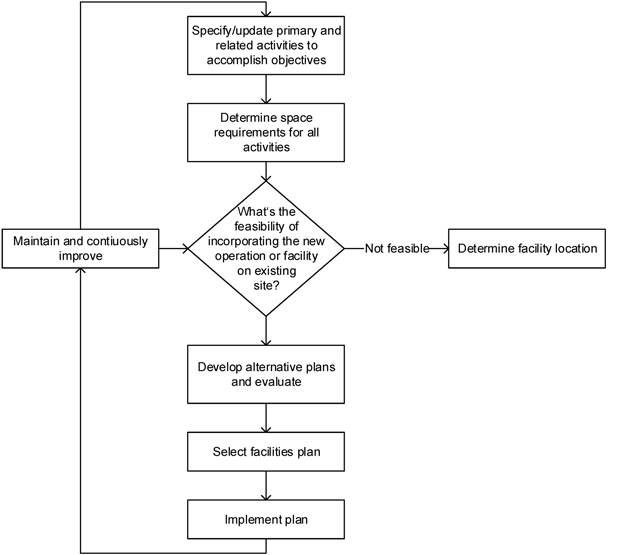
Fig. 2. Continuous improvement facilities planning cycle, Tompkins et al. (2010).
Due to the interaction between the areas assigned in the log yard during facility planning, the placement of machines and the delivery points, the underlying optimisation problem is quadratic.
A discrete method to solve the facility layout problem is the quadratic assignment problem which is introduced by Koopmans and Beckmann (1957). By this, the layout and the referable units are divided into equally sized squares and each square is assigned to one storage area square. The objective of the quadratic assignment problem is to minimise the travelled distance Djk of connected locations with the number of transportation runs Ahi, given by the transported volume. The decision variable xhj tells which locations should be connected to each other and where which raw material should be stored considering the resulting material flow between the locations.
![]()
![]()
![]()
![]()
The problem is linear and therefore easier if there are no interactions between the areas which have to be assigned and if delivery point and material charge are already fixed. The model for the linear assignment problem is introduced in the next section. Thus, dependent and independent storage assignment problems have to be distinguished and the appropriate solution method for the problem needs to be used. To highlight one existing heuristic to plan a layout, the slicing tree algorithm is presented. Here, a continuous area is separated with horizontal or vertical Guillotine-cuts. The major advantage of this heuristic is the possibility to simultaneously plan a suitable driveway system within the layout. These driveways have minimal crossroads and no dead ends which lead to a total improvement in accessibility. The quadratic assignment problem or the slicing tree approach are two possible ways to solve the facility layout problem. In Scholz et al. (2009) the authors introduce a heuristic based on slicing tree and Tabu search. The introduced heuristic seems to be superior to existing heuristics and promising for solving large problems in reasonable time.
3.3 Storage assignment
After obtaining the general layout of the log yard and the placement of fixed objects such as measuring unit, sorting line, sawing lines and dry kilns the continuous improvement cycle proceeds with the storage assignment for all assortments. As assortments change over time with volume variations, the introduction of new assortments and seasonal variations, the optimal storage assignment is modified. Similarly, external conditions such as supplies, demands, products and technologies may vary too. Consequently, re-evaluating the existing storage assignment and optimising it is crucial.
As there is usually no interaction between storage areas the original problem of storage assignment is linear, as already introduced by Koopmans and Beckmann (1957), and again the distance travelled is minimised.
![]()
![]()
![]()
![]()
When the main layout of the log yard and its key features such as placements of machines, the sorting line, the grading and measurement station are fixed the optimisation potential lies in the reassignment of storage areas.
Contrary to the common log yard the next paper presented investigates a log yard using a gantry crane instead of log stackers to sort the material into storage areas and feed the saw, which makes the transportation aspect within the log yard much easier. Rathke et al. (2013) use mathematical programming and heuristics to improve the internal logistics of the log yard with a given layout of a medium sized European hardwood sawmill. The log yard layout planning problem in general includes two different assignment decisions. First, each assortment has to be assigned to one ejection box along the sorting line according to diameter, length and wood type and secondly, each assortment has to be assigned to one or more storage areas. By rearranging the box assignment for different assortments and assigning the optimal storage areas for the material, the total transportation time of the crane can be decreased for one production cycle of 15 days. Moreover, a redesign of the log yard reducing the number of storage areas by combining some of them is investigated. The authors develop two optimisation approaches. The first approach divides the problem into two separate assignment problems and solves the storage box assignment first, whereas the second approach solves the two problems concurrently. The best solution, with a reduction of transportation time by 16 percent, can be reached when reducing the number of storage areas, thereby enlarging the maximal capacity of some storage areas and solving the allocation problem of ejection boxes along the sorting line and storage areas simultaneously. The authors state that the model finds a good solution within seconds but proving optimality is hard because of the similar volumes of the different log assortments and the similar capacities of the storage areas. Thus, the heuristics are seen as an easy way to reduce the transportation time without the need of sophisticated optimisation tools.
Contrary to the aforementioned, the paper by Rahman et al. (2014b) proposes a discrete event simulation approach to improve the log yard and its processes. By this, the storage bins are rearranged to effectively minimise the log stacker time. Due to computational limits, not all possible arrangement options of the combinatorial optimisation are investigated but metaheuristics are incorporated. Therefore, they investigate a genetic algorithm and compare it to a simulated annealing approach. These two improvement methods were checked against the existing layout. Due to the smaller investigated solution space of simulated annealing, the genetic algorithm is better suited for this problem. Additionally, different random arrival patterns of logs have been studied. The models are applied to a sawmill log yard in Sweden with an annual production of about 400 000 m³.
The aforementioned problems describe principal challenges on the log yard. In the following section more specific questions and problems such as the material movement in the log yard, which loaders are used and assigned to which tasks together with the robustness of the solutions for varying data are discussed. Nevertheless, understanding the material flow on the log yard, knowing the facility layout of the production site and being aware of the storage assignment is essential for a more detailed analysis of log yard logistics.
4 Operational problems
4.1 Material movement
Transportation operations are a significant cost for the primary wood industry. Audy et al. (2012) give a thorough overview of existing planning methods and support systems for the vehicle routing problem for timber transportation. This review study however does not include the internal transportation on a log yard, the analysis of how many loaders are necessary for a continuous production, the allocation of duties, the planning of reserve capacities and maintenance planning, shift models and scheduling of loaders.
Baesler et al. (2002) propose a simulation optimisation methodology applied to a production line for a secondary manufacturing wood processing plant in Chile. Their simulation model is integrated into a genetic algorithm heuristic and studies different resource configurations for the plant. The authors are able to optimise the number of forklift cranes within the production line. The average time required to finish the complete cycle of a product can be decreased by approximately 18 percent by increasing the number of forklift cranes by four as they are basically in charge of transporting material from one working centre to the next and constitute a bottleneck of the process flow. The increase creates a more synchronised system. A further study of the layout and the increased forklift crane flow has to be conducted to guarantee the feasibility of the proposed solution.
Beaudoin et al. (2012) investigate different loader to truck allocation strategies and their influence on truck cycle time and loader driving distance on the log yard using discrete event simulation. The sawmill examined, with an annual consumption of 600 000 m³, handles up to 140 log trucks per day and is located in the western part of Canada. The authors compare the current practice of first-in-first-out to empty-the-queue-first and longest-queue-first allocation strategy for the log trucks. While empty-the-queue-first leads to an average decrease in truck cycle time and loader driving distance, the longest-queue-first approach has no significant impact on the truck cycle time but increases the average total distance travelled compared to the first-in-first-out approach. A sensitivity analysis on mill consumption rate and travelling speed of loaders was conducted. However, the authors mention that both newly introduced and analysed approaches have a higher variance in waiting time. Furthermore, no distinction between trailer types was investigated though this would allow comparison of individual truck wait time per trailer type among the allocation strategies.
Another simulation approach to increase the efficiency of log yard operations is conducted by Shaik et al. (2012). In their work they develop efficient work order decisions for two log stackers at a Swedish sawmill and compare three different scenarios with the conventional approach by multi-agent based simulation. The first approach is to increase the buffer on the measurement station by one to three segments, thereby providing more time for the log stackers in between unloading trucks. The second approach prohibits the unloading of trucks to the ground as an artificial buffer space for the measurement station. Thus, the waiting time of trucks is increased which leads to high demurrage fees which have to be paid by the sawmill. For both of these approaches the responsibilities of the log stackers stay the same as in the conventional approach where both stackers are doing the same tasks but with different priorities. For the third approach the responsibilities of unloading trucks, filling the measurement station, feeding the sawmill and emptying the storage bins along the sorting conveyer belt are split between the two log stackers. However, compared to the conventional approach the buffer size does not change. The authors conclude that prohibiting unloading to the ground is better but the waiting time will therefore be increased. Furthermore, it is better to divide the work load between the two stackers if the physical layout is not changed. Hence, Approach 3 is superior to the status quo. Approach 2 and 3 lead to a significant improvement because the performance of the sawmill depends directly on the speed at which the buffer is filled.
Investigating the material movement and vehicle routing problem on the log yard, assigning specific duties to each vehicle and analysing different shift models to synchronise the vehicle capacity to the production capacity is the next step in optimising logistics within the log yard after establishing the layout. For this problem simulation is a suitable solution method to study the given problem or question.
4.2 Empty trips
All the aforementioned methods and the papers presented minimise the distance of loaded trips whereas the empty trips are neglected. Arnold and Furmans (2006) propose a method to determine the number of empty trips in the best-case scenario. With the solution of the optimised loaded runs from the storage assignment problem, the transportation matrix λij is calculated. This matrix gives the number of loaded runs from location i to location j. In a next step source (Hisource) and sink (Hjsink) characteristics of each location are calculated.
![]()
![]()
With the transportation matrix the number of trips starting and ending at one unit can be computed. Consequentially, it can be determined if there is supply or demand of vehicles in one specific location.
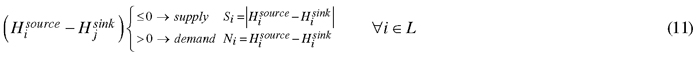
Thus, the total distance of empty runs, where δij are the number of empty runs, can be computed when the supply and demand of vehicles need to be balanced at each location.
![]()
![]()
![]()
![]()
This concept is introduced by Arnold and Furmans (2006). As mentioned before this is an approach to estimate empty trips as it minimises the distance of unproductive trips for the best-case scenario, therefore giving a lower bound on empty trips. Another option to investigate and evaluate the empty runs is to simulate the total vehicle movement within the log yard taking the delivery rate of raw material, the production rate of the saws and all other duties of the loaders into considerations. Consequentially these analyses and solutions lead to a routing and dispatch system for the log yard indicating the next task which has to be performed for each vehicle.
Generally in literature, the empty trips on the log yard are not taken into account, but among others two papers on the supply chain planning to the log yard which deal with the minimisation of empty trips were found. Gronalt and Hirsch (2007) introduce a Tabu search based method to reduce overall duration of empty truck movements for the round wood transport whereas the paper by El Hachemi et al. (2011) investigates the potential of both constraint programming and mathematical programming for the log truck scheduling. The total costs of non-productive activities and distances driven empty by vehicles are minimised. But the aforementioned literature does not take the empty trips within the log yard itself into account.
4.3 Seasonality and raw material supply
The first problem is to determine how much raw material should be stored in the log yard throughout the year. The stock level should adapt to the material inflow and this is normally kept high to maintain feedstock for continuous production and ensure low setup cost for production. The chip pile management for any mill that stores chips is discussed by Fuller (1985). The author highlights the history of pile storage for chips used in wood products which is required to handle the intermittent flow and is maintained over several periods especially when the supply is low, e.g. during winter or rainy seasons. The paper reviews practices to avoid deterioration and economic losses caused by chip storage. Dramm et al. (2004) on the other hand discuss the problem of excessive log inventory and storage at log yards. The authors examine the trade-off between reducing bottlenecks to improve mill productivity and keeping the inventory low. Finally, they conclude that companies may have to maintain a generally large inventory that fluctuates with the season. Motivated by the raw material management at a sawmill Silver and Zufferey (2005) develop a heuristic method for inventory management. With Tabu search and simulation, the expected costs of lost sales facing a known and constant demand rate is minimised. However, the lead times are random and moreover the probability distribution of the lead times change in a seasonal fashion.
There are several ways to deal with seasonality reflected in data. One possibility is to solve the layout and assignment problem for the largest volume to ensure an optimal assignment when the log yard is used to its capacity. Marasini et al. (2001) propose an integrated simulation model which uses artificial intelligence methods to solve the problem of designing and managing a make-to-stock stockyard layout for the concrete products industry with seasonal demand. Another way is to indicate the best enhancement strategies for the different assortments of the log yard. Therefore, the storage assignment problem is solved for average volumes and the storage areas used are fixed. In a next step the volumes are increased and the next best location for each assortment is computed thus indicating where the additional material should be stored if the usual volume is exceeded.
A further way to solve the seasonality problem is to solve the assignment problem from the previous section over several periods and to enhance the objective function by a marshalling component to always ensure the optimal solution of the problem. This additional component represents the costs of reassigning storage areas and the time it takes to alter an existing layout. The concept of re-marshalling is well known in the area of container handling in port container terminals. Kim and Bae (1998) describe a methodology to convert an existing layout to a desirable one with the fewest possible moves and the shortest possible travel distance. They divide the problem into the three sub-problems of: finding the desired layout, planning the move and sequencing the tasks to be performed. The problem of re-marshalling within a limited time frame is solved by Yu and Qi (2013). Here they solve the problem with a heuristic algorithm to restore the optimised space allocation. This concept can be easily adapted to the log yard layout planning.
In existing literature there are two papers investigating seasonal effects on the log yard design. For the log yard design and yard performance evaluation Robichaud et al. (2014) examine a discrete event simulation applied to a medium sized lumber mill log yard in Quebec with an annual consumption of 500 000 m³. Their work is based on the research of Hampton (1981) about planning, construction and operation of dry land log yards and the work of Baker and Canessa (2009) on a structured approach for a warehouse design. After collecting relative data Robichaud et al. (2014) model the material flow and establish flow priorities. Furthermore, space needed for each activity is determined and preliminary plans are proposed and tested with the proposed simulation model. This is similar to the steps introduced by Hampton (1981) but extended by the final simulation. These crucial steps are generally valid but here different data sets are investigated to simulate the seasonality of the problem. The simulation model is tested for one layout with equipment combinations for high and low utilization and arrival rates. The key performance indicators are scheduled time utilization and total travelled distance. A noticeable improvement in the distance travelled can be achieved by relocating the slashing station. Furthermore, the authors conclude that there was a potential saving of one loader during spring time, which is the time with fewer arrivals.
The paper above by Rahman et al. (2014b) also investigates the storage assignment with seasonal data. As they assign dynamic storage bins, the effects on changing data and therefore varying transport volume can be studied. They compare the solutions of two different data sets. One is a one-month planning sample and the other a three-month planning sample covering the one-year planning horizon. Compared to the existing layout, the saving potential on distance travelled by log stackers with the improved storage assignment is better for the three-month planning sample. The authors conclude that the distance increases even more for a larger input sample size and therefore the potential of optimisation increases as well.
Dealing with seasonal data is never easy but it is even more important for the forest-based industries because of the quantity of raw material and the disparity between high and low arrival rates.
Next, in order to supplement the work referenced, several case studies are discussed using some of the models presented above.
5 Case studies
5.1 Sawmill A
The sawmill investigated, with an annual production volume of around 100 000 m³ mainly processes large dimensional timber. It has three different sawing techniques, a gang saw, a band saw and a profiler. Additionally, an automatic sorting and packing facility and several dry kilns are at its disposal to produce 16 different product categories. Situated on both sides of a main road (Fig. 3), it has within it eight different vehicles to manage the internal logistics of logs and sawn timber which together cover approximately 8500 kilometres per month. The forklift movements during the production process are shown in Fig. 4.

Fig. 3. Layout of the sawmill bisected by a main road, © GIS Steiermark, 2017, www.gis.steiermark.at.
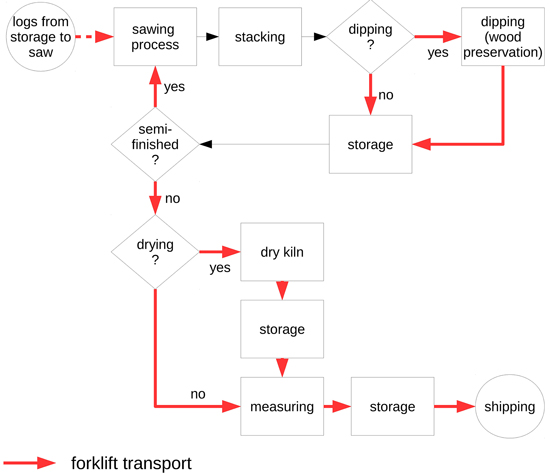
Fig. 4. Forklift resource scheduling logic during the production process.
In order to improve the overall log yard logistics, the storage assignment is initially recalculated with a two-opt-heuristic where two storage areas are switched when the required storage space differs between the two assortments by at most a third of the space. This approach is based on the work of Buffa et al. (1964). The authors propose a heuristic where facilities are allocated and pairwise exchanged to minimise the transportation costs. A further improvement for the overall material flow within the log yard can be obtained by installing a central unloading station next to the main road alongside the sawmill which can be identified by use of simulation. Central unloading would reduce main road crossing (Table 4).
| Table 4. Potential savings of improved storage assignment and centrally located unloading station in comparison to the existing layout. | ||||
| Original layout | Central unloading | |||
| Distance | Crossings | Distance | Crossings | |
| Status quo | 27 705 km | 28 896 | 27 984 km | 30 090 |
| New assignment | 25 339 km | 24 207 | 25 706 km | 25 401 |
| Possible improvement | 2366 km | 4689 | 2277 km | 4689 |
| Savings | 8.5% | 16.2% | 8.1% | 15.6% |
| Savings compared to original layout | 7.2% | 12.1% | ||
The final part of the study is to optimise the routing and dispatch of the forklifts and synchronise them with the production schedule. Additionally, the efficiency of the transport processes, the utilization of the forklifts and the transport distances are analysed. Thus, an agent-based discrete event simulation model is used with the underlying data of production volume, product mix, production processes and sales and purchases of both raw and sawn timber. Several different shift scenarios are tested and compared to the status quo. With the simulation model the company is able to eliminate one of the forklifts and distribute the workload to the other remaining vehicles evenly. Moreover, the total distances covered both of loaded and empty runs can be reduced due to improved forklift dispatch.
5.2 Sawmill B
Another sawmill has annual production capacity of about 250 000 m³ and is the first part in a long value chain producing glued laminated timber that finds wide use in the wood construction industry. The current situation of the log yard storage assignment is compared to an optimised one where the sorting capacity, the production capacity of the saw and the capacity of the loaders are taken into consideration. Additionally, a new position for the material charge is investigated to provide easier access for the loaders. The optimisation model is based on the storage assignment model, in Section 3.3 by Rathke et al. (2013) where the transportation distance between ejection boxes, storage boxes and material charge is minimised. The initial log yard layout and the position of material charge are shown in Fig. 5.

Fig. 5. Log yard layout of the sawmill investigated with a sorting line on the bottom left corner with 40 ejection boxes, storage areas located at the upper left corner alongside a tree line where the debarked logs are stored and the material charge on the top right corner of picture, © GIS Steiermark, 2017, www.gis.steiermark.at.
In addition, the average grapple utilization of the loaders is determined and the possible savings with an improvement of this utilization is studied. The results of savings in operating hours for different scenarios are listed in Table 5.
| Table 5. Saving in operating hours for different grapple utilization and scenarios for all vehicles on the log yard. | ||||||
| Grapple utilization | 56% | 60% | 70% | 80% | 90% | 100% |
| Status quo | 0% | 4% | 11% | 16% | 20% | 24% |
| Optimised | 5% | 8% | 14% | 18% | 22% | 25% |
| Relocation of material charge | 7% | 10% | 18% | 23% | 27% | 31% |
| Relocation and optimised | 12% | 15% | 22% | 26% | 30% | 33% |
The grapple capacity utilization of 100 percent is the theoretical upper bound which will never be actually possible on a log yard. Nevertheless, to increase the actual grapple utilization the company wants to install a routing and dispatch system to determine which ejection box along the sorting line needs to be emptied next. This enables the loader drivers within the log yard to follow a schedule which enhances their work performance. The management of the company anticipates an average usage of approximately 80 to 85 percent of the grapple capacity. Even so, the operating hours can be reduced by at least 7 percent by relocating the material charge without altering the existing storage assignment consequently this is the first step the company will implement in the log yard.
5.3 Panel industry A
The next case study investigates the layout problem for the log yard of a large European panel producer. The first step studies the material flow and sets target values for each assortment. Subsequently this is used to determine how much space each assortment requires in the log yard. These target values are determined by the purchasing and production departments of the project partner. Optimising the log yard layout using these values produces an ideal layout. Within this panel producer’s site the material flow is more complicated as there are three different delivery points, all with the possibility of pre-processing and three different material charges. The current layout is compared to an optimisation approach where the storage space used is rearranged and also to an approach where all the free space is taken into consideration. These two optimisation approaches serve as a lower and upper bound for the feasible new layout for the industrial partner. Considering that the location of material charge, machines and feedings are known and constant we again use the linear storage assignment problem introduced in Section 3.3. As a next step the minimal empty runs are estimated. This computation for each vehicle is based on Arnold and Furmans (2006) where the authors give a method to minimise the empty runs as described in Section 4.2. Several different scenarios and combinations are tested. With the final layout yearly transportation costs can be reduced by approximately 32 percent. This can be achieved by eliminating empty movements and the rearrangement of the storage spaces. For the project partners the illustration of the material flow in the log yard with a Sankey diagram, introduced in Section 3.1, is an everyday tool used for better understanding (Fig. 6).
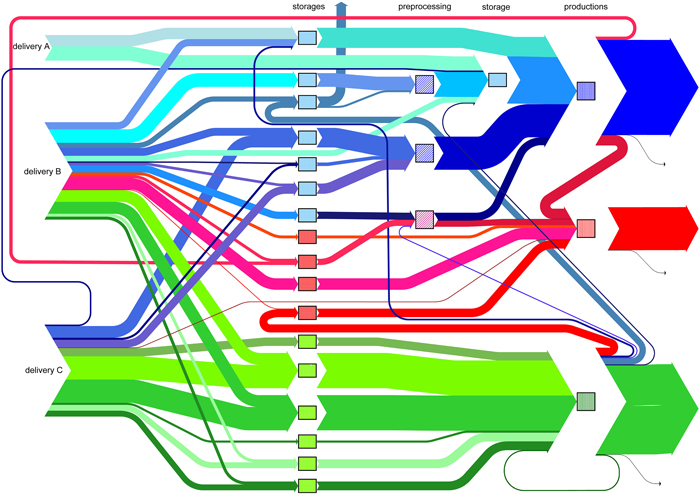
Fig. 6. Internal material flow within the log yard of a panel producer where the material is delivered at three different locations and distributed to different storage areas on the log yard depending on the assortment and geometry of the raw material, with pre-processing if needed, waste management, different production sites, indicated with different colours and discarded material. View larger in new window/tab.
5.4 Panel industry B
The next case study deals with chip board industry and investigates the material flow in the log yard taking into account new processes and plant renovations. The existing layout is compared to the solution obtained by assigning new storage areas for the raw materials sequence according to the required number of transportation runs. Thus, the raw material with the highest number of transportation runs is assigned to the storage area with the closest distance to the material charge. This heuristic assignment approach is described in Askin and Standridge (1993) where elements are assigned in a 3-dimensional space. Therefore, the storage areas used are rearranged to minimise the overall travel distance and thus reducing transportation by approximately 8 percent. Moreover, additional storage areas are investigated by dividing the space into a grid and assigning the raw material according to the number of transportation runs needed. Here all free areas on the log yard are considered to be available for storage. In this way the transportation runs can further be minimised by 26 percent. Finally the plant was renovated and the resulting new material flow investigated which showed that the total number of transportation runs could be reduced by 33 percent mainly by pre-processing chips and recycled wood. The improved storage arrangement with indicated storage areas is shown in Fig. 7.
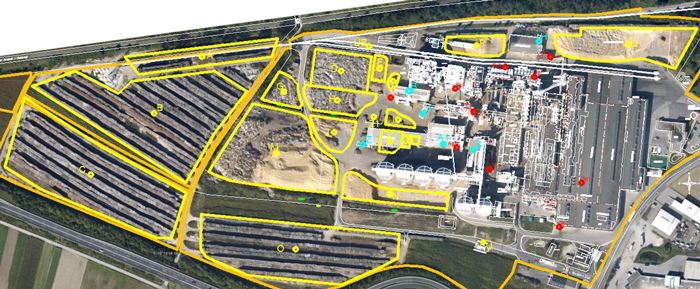
Fig. 7. Layout and storage assignment of sample chip board industry with storage areas indicated in yellow for different geometries of raw material, locations of material charges in turquoise and locations where recycling material accrues in red. View larger in new window/tab.
6 Conclusion and further research
This paper introduced a structural approach to the log yard logistics problem. The different planning problems which affect the log yard, namely tactical structural and operational problems, are described. Additionally, the existing literature on these topics according to the aforementioned classification is listed. Given the size of log yards in the wood industry, the complexity of their material flow, the variety of stored geometries and vehicles required as well as the seasonality of the raw material inflow, great potential lies in the optimisation of log yard logistics. Further, due to the constantly changing externalities such as supply, demand, products and technologies, a continuous improvement cycle is mandated. When considering the importance and repetitive necessity of planning log yard logistics it is surprising that so little research has been conducted.
The first step needed to improve the internal logistics of a log yard is to study and understand the existing material flow. Moreover, the facility layout and the storage assignment can be analysed and improved. With this information the actual vehicle movement and the empty trips within the log yard can be planned. In addition, the appropriateness of the solution can be tested for seasonally varying data. Depending on whether the problem is dynamic or static, either optimisation, simulation or heuristics may be more suitable. In the second part of the paper several case studies using different methods are described and varying problems of log yard logistics are studied. The first case study optimises the storage assignment with a two-opt heuristic and solves the routing and dispatch of forklifts by analysing different shift models and utilization rates of the vehicles with a discrete event simulation. In the next two sawmill case studies, the storage assignment can be optimised with a linear model as described in Section 3.3. Additionally, the benefits of a routing and dispatch system were analysed with the linear optimisation model applied to the second case study. Contrary to the first two case studies, the third case study, Panel industry A, illustrates material flow with a Sankey diagram. The last case study, Panel industry B, investigates changes in the log yard and investment potential with the help of a simple heuristic.
As mentioned before there are several different approaches to solving the investigated problems. For future work the focus should be on the analysis and implementation of routing and dispatch systems in the log yard as these have the greatest potential. Another interesting problem is to synchronise the shift scheduling of loaders with the production program. Due to smaller diameter logs on the sawmill fewer trips are needed to supply the saw because with one trip more material can be transported. Moreover, the throughput per hour decreases so fewer vehicles are required for sawn timber. In addition, the dry kiln scheduling, especially the loading and unloading of each dry kiln, can be synchronised with the availability of vehicle capacity and planned according to the loader schedule. Furthermore, for the primary wood industry, the sensitivity of the solutions to seasonal data needs to be studied or seasonality models with a marshalling factor implemented. Finally, new transport systems and automation of the log yard can be considered in order to bring the next industrial revolution to the log yard.
Acknowledgment
The authors want to thank their colleagues Matthias Kaltenbrunner and Martin Pernkopf who have been involved in projects which are included in the case studies.
References
Abotaleb I., Nassar K., Hosny O. (2016). Layout optimization of construction site facilities with dynamic freeform geometric representations. Automation in Construction 66: 15–28. https://doi.org/10.1016/j.autcon.2016.02.007.
Arnold D., Furmans K. (2006). Materialfluss in Logistiksystemen. Springer Berlin Heidelberg, [Material flow in logistical systems].
Askin R.G., Standridge C.R. (1993). Modeling and analysis of manufacturing systems. John Wiley & Son.
Audy J.-F., D’Amours S., Rönnqvist M. (2012). Planning methods and decision support systems in vehicle routing problems for timber transportation: a review. Vol. 45. CIRRELT Montreal, Canada.
Audy J.F., Marques A.S., Rönnqvist M., Epstein R., Weintraub A. (2014). Transportation and routing. Springer Netherlands, Dordrecht. p. 269–295. https://doi.org/10.1007/978-94-017-8899-1_8.
Baesler F.F., Moraga M., Ramis F.J. (2002). Productivity improvement in the wood industry using simulation and artificial intelligence. In: Proceedings of the 34th Conference on Winter Simulation: Exploring New Frontiers, WSC ‘02. Winter Simulation Conference. p. 1095–1098. https://doi.org/10.1109/WSC.2002.1166362.
Baker P., Canessa M. (2009). Warehouse design: a structured approach. European Journal of Operational Research 193(2): 425–436. https://doi.org/10.1016/j.ejor.2007.11.045.
Balakrishnan J., Cheng C.-H., Wong K.-F. (2003). Facopt: a user friendly facility layout optimization system. Computers & Operations Research 30(11): 1625–1641. https://doi.org/10.1016/S0305-0548(02)00096-5.
Beaudoin D., LeBel L., Soussi M.A. (2012). Discrete event simulation to improve log yard operations. INFOR: Information Systems and Operational Research 50(4): 175–185. https://doi.org/10.3138/infor.50.4.175.
Bouchard M., D’Amours S., Rönnqvist M., Azouzi R., Gunn E. (2017). Integrated optimization of strategic and tactical planning decisions in forestry. European Journal of Operational Research 259(3): 1132–1143. https://doi.org/10.1016/j.ejor.2016.11.022.
Buffa E.S., Armour G.C., and Vollmann T.E. (1964) Allocating facilities with CRAFT. Harvard Business School 42(2): 136–158.
D’Amours S., Rönnqvist M., Weintraub A. (2008). Using operational research for supply chain planning in the forest products industry. INFOR Information Systems and Operational Research 46(4): 265–281. https://doi.org/10.3138/infor.46.4.265.
Dramm J.R., Govett R., Bilek T., Jackson G.L. (2002). Review of log sort yards. US Department of Agriculture, Forest Service, Forest Products Laboratory. 39 p. https://doi.org/10.2737/FPL-GTR-132.
Dramm J.R., Govett R., Bilek T., Jackson G.L. (2004). Log sort yard economics, planning, and feasibility. US Department of Agriculture, Forest Service, Forest Products Laboratory. 31 p. https://doi.org/10.2737/FPL-GTR-146.
Drira A., Pierreval H., Hajri-Gabouj S. (2007). Facility layout problems: a survey. Annual Reviews in Control 31(2): 255–267. https://doi.org/10.1016/j.arcontrol.2007.04.001.
El Hachemi N., Gendreau M., Rousseau L.-M. (2011). A hybrid constraint programming approach to the log-truck scheduling problem. Annals of Operations Research 184(1): 163–178. https://doi.org/10.1007/s10479-010-0698-x.
Fuller W.S. (1985). Chip pile storage – a review of practices to avoid deterioration and economic losses. Tappi Journal 68(8): 49–52.
Gendron B., Pulkki R., Posta M., Favreau J. (2016). Forest value chain optimization and sustainability, chapter overview of wood transportation and operations research methods in this area. CRC Press. p. 311–330.
Gronalt M., Hirsch P. (2007). Log-truck scheduling with a tabu search strategy. Vol. 39. Springer. p. 65–88.
Gronalt M., Rauch P. (2018). Analyzing railroad terminal performance in the timber industry supply chain – a simulation study. International Journal of Forest Engineering. 9 p. https://doi.org/10.1080/14942119.2018.1488913.
Gupta T., Seifoddini H.I. (1990). Production data based similarity coefficient for machine-component grouping decisions in the design of a cellular manufacturing system. International Journal of Production Research 28(7): 1247–1269. https://doi.org/10.1080/00207549008942791.
Hampton C.M. (1981). Dry land log handling and sorting: planning, construction, and operation of log yards. M. Freeman Publication.
Huka M.A., Gronalt M. (2017). Model development and comparison of different heuristics for production planning in large volume softwood sawmills. Engineering Optimization 49(11): 1829–1847. https://doi.org/10.1080/0305215X.2016.1271882.
Kazemi Zanjani M., Nourelfath M., Ait-Kadi D. (2010). A multistage stochastic programming approach for production planning with uncertainty in the quality of raw materials and demand. International Journal of Production Research 48(16): 4701–4723. https://doi.org/10.1080/00207540903055727.
Kim K.H., Bae J.W. (1998). Re-marshaling export containers in port container terminals. Computers & Industrial Engineering 35(3): 655–658. Selected Papers from the 22nd ICC and IE Conference. https://doi.org/10.1016/S0360-8352(98)00182-X.
Koopmans T.C., Beckmann M. (1957). Assignment problems and the location of economic activities. Econometrica 25(1): 53–76. https://doi.org/10.2307/1907742.
Kusiak A., Heragu S.S. (1987). The facility layout problem. European Journal of Operational Research 29(3): 229–251. https://doi.org/10.1016/0377-2217(87)90238-4.
Lebedys A., Li Y. (2014). Contribution of the forestry sector to national economies, 1990–2011. Forest Economics, Policy and Products Division, Forestry Department, Food and Agriculture Organization of the United Nation.
Marasini R., Dawood N.N., Hobbs B. (2001). Stockyard layout planning in precast concrete products industry: a case study and proposed framework. Construction Management and Economics 19(4): 365–377. https://doi.org/10.1080/01446190110035636.
Maturana S., Pizani E., Vera J. (2010). Scheduling production for a sawmill: a comparison of a mathematical model versus a heuristic. Computers & Industrial Engineering 59(4): 667–674. https://doi.org/10.1016/j.cie.2010.07.016.
Minard C.-J. (1844/1870). Des Tableaux graphiques et cartes figuratives. Bibliotèque numérique patrimoniale des ponts et chaussées. [Graphic displayboards and figurative maps].
Muther R. (1973). Systematic layout planning. Cahners Book.
Page A.L. (1991). New product development survey: performance and best practices. In: PDMA Conference, Chicago. Vol. 13.
Rahman A., Yella S., Dougherty M. (2014a). Simulation and optimization techniques for sawmill yard operations – a literature review. Journal of Intelligent Learning Systems and Applications 6(1): 21–34. https://doi.org/10.4236/jilsa.2014.61003.
Rahman A., Yella S., Dougherty M. (2014b). Simulation model using meta heuristic algorithms for achieving optimal arrangement of storage bins in a sawmill yard. Journal of Intelligent Learning Systems and Applications 6(2): 125–139. https://doi.org/10.4236/jilsa.2014.62010.
Rathke J., Huka M.A., Gronalt M. (2013). The box assignment problem in log yards. Silva Fennica 47(3) article 1006. https://doi.org/10.14214/sf.1006.
Robichaud S.V., Beaudoin D., LeBel L. (2014). Log yard design using discrete-event simulation: First step towards a formalized approach. In MOSIM 2014, 10ème Conférence Francophone de Modélisation, Optimisation et Simulation.
Rönnqvist M. (2003). Optimization in forestry. Mathematical programming 97(1–2): 267–284. https://doi.org/10.1007/s10107-003-0444-0.
Sankey H.R. (1898). The thermal efficiency of steam engines. Report of the committee appointed to the council upon the subject of the definition of a standard or standards of thermal efficiency for steam engines: with an introductory note. Minutes of the Proceedings of the Institution of Civil Engineers 134(1898): 278–312. Plate 5.
Santa-Eulalia L.A., D’Amours S., Frayret J.-M. (2012). Agent-based simulations for advanced supply chain planning and scheduling: the FAMASS methodological framework for requirements analysis. International Journal of Computer Integrated Manufacturing 25(10): 963–980. https://doi.org/10.1080/0951192X.2011.652177.
Schmidt M. (2008). The sankey diagram in energy and material flow management, part I: history. Journal of Industrial Ecology 12(1): 82–94. https://doi.org/10.1111/j.1530-9290.2008.00004.x.
Scholz D., Petrick A., Domschke W. (2009). Stats: a slicing tree and tabu search based heuristic for the unequal area facility layout problem. European Journal of Operational Research 197(1): 166–178. https://doi.org/10.1016/j.ejor.2008.06.028.
Shaik A.u.R., Vlad S., Rebreyend P., Yella S. (2012). Multi-agent simulation of sawmill yard operations. In: Bruzzone A., Hamza M.H. (eds.). ASM-ASC 2012 - applied simulation and modelling – artificial intelligence and soft computing. https://doi.org/10.2316/P.2012.776-043.
Silver E.A., Zufferey N. (2005). Inventory control of raw materials under stochastic and seasonal lead times. International Journal of Production Research 43(24): 5161–5179. https://doi.org/10.1080/00207540500219866.
Singer M., Donoso P. (2007). Internal supply chain management in the Chilean sawmill industry. International Journal of Operations & Production Management 27(5): 524–541. https://doi.org/10.1108/01443570710742393.
Singh S.P., Sharma R.R.K. (2006). A review of different approaches to the facility layout problems. The International Journal of Advanced Manufacturing Technology 30(5): 425–433. https://doi.org/10.1007/s00170-005-0087-9.
Tompkins J.A., White J.A., Bozer Y.A., Tanchoco J.M.A. (2010). Facilities planning. John Wiley & Son.
Vergara F.P., Palma C.D., Sepúlveda H. (2015). A comparison of optimization models for lumber production planning. Bosque 36(2): 239–246. https://doi.org/10.4067/S0717-92002015000200009.
Yu M., Qi X. (2013). Storage space allocation models for inbound containers in an automatic container terminal. European Journal of Operational Research 226(1): 32–45. https://doi.org/10.1016/j.ejor.2012.10.045.
Yujie Z., Fang W. (2009). Study on the general plane of log yards based on systematic layout planning. In: ICIII ‘09 Proceedings of the 2009 International Conference on Information Management, Innovation Management and Industrial Engineering, vol. 3. p. 92–95. https://doi.org/10.1109/ICIII.2009.332.
Total of 50 references.

