Within-tree radial and among-family variations in wood density, microfibril angle, and mechanical properties in Picea glehnii
Tanabe J., Ishiguri F., Tamura A., Takashima Y., Ohshima J., Iizuka K., Yokota S. (2018). Within-tree radial and among-family variations in wood density, microfibril angle, and mechanical properties in Picea glehnii. Silva Fennica vol. 52 no. 2 article id 9914. https://doi.org/10.14214/sf.9914
Highlights
- The modulus of elasticity was affected by both microfibril angle and wood density, whereas the modulus of rupture was mainly affected by wood density in Picea glehnii
- A larger degree of among-family variation in wood properties was detected in juvenile wood than in mature wood, indicating that genetic improvements in the mechanical properties may be more effective for juvenile wood.
Abstract
Genetic improvements in the mechanical properties of wood are important in forestry species used for lumber, such as Picea. The within-tree radial and among-family variations for the modulus of elasticity (MOE), modulus of rupture (MOR), and their related traits [i.e., microfibril angle (MFA) of the S2 layer in latewood tracheid and air-dry density (AD)] were evaluated in nine open-pollinated families of Picea glehnii (F. Schmidt) Mast. The radial variation in MOR was mainly affected by AD, whereas MOE was affected by MFA and AD. Higher F-values obtained by analysis of variance and coefficient of variation were observed for all properties at the 6th–15th annual ring, except for AD at the 6th–10th annual ring. This result suggests that the contribution of genetic effect is larger in these highly variable regions. In addition, positive correlation coefficients were obtained between wood properties at the 6th–15th annual ring and mean values of these properties. Therefore, genetic improvements for MOE, MOR, and their related traits in P. glehnii is likely to be more effective in juvenile wood, specifically at the 6th–15th annual ring from the pith.
Keywords
modulus of elasticity;
modulus of rupture;
early selection;
tree breeding for wood quality
-
Tanabe,
Faculty of Education, Chiba University, Chiba, 263-8522, Japan
E-mail
tanabe_j@chiba-u.jp

- Ishiguri, Faculty of Agriculture, Utsunomiya University, Utsunomiya 321-8505, Japan E-mail ishiguri@cc.utsunomiya-u.ac.jp
- Tamura, Forest Tree Breeding Center, Forestry and Forest Products Research Institute, Hitachi, 319-1301, Japan E-mail akirat@affrc.go.jp
- Takashima, Forest Tree Breeding Center, Forestry and Forest Products Research Institute, Hitachi, 319-1301, Japan E-mail ytakashima@ffpri.affrc.go.jp
- Ohshima, Faculty of Agriculture, Utsunomiya University, Utsunomiya 321-8505, Japan E-mail joshima@cc.utsunomiya-u.ac.jp
- Iizuka, Faculty of Agriculture, Utsunomiya University, Utsunomiya 321-8505, Japan E-mail kiizuka@cc.utsunomiya-u.ac.jp
- Yokota, Faculty of Agriculture, Utsunomiya University, Utsunomiya 321-8505, Japan E-mail yokotas@cc.utsunomiya-u.ac.jp
Received 24 November 2017 Accepted 2 February 2018 Published 7 February 2018
Views 102588
Available at https://doi.org/10.14214/sf.9914 | Download PDF

1 Introduction
The genus Picea is one of the most important for forestry use in the boreal zone of Japan as well as in northern European and North American countries. A total of seven Picea species are naturally distributed in Japan (Farjon 1990). Of these, Picea glehnii (F. Schmidt) Mast. is considered the most important for wood production in Hokkaido (Japan) because it is highly resistant to damage caused by late spring frosts and to rat attacks (Myodes rufocanus bedfordiae Thomas) compared with other species, such as Abies sachalinensis (F. Schmidt) Mast. or Larix kaempferi (Lamb.) Carrière (Kita 2008). P. glehnii has been targeted for tree breeding programs in Japan (Ohba and Katsuta 1991; Kita 2008).
Because P. glehnii wood is mainly used as construction lumber, the modulus of elasticity (MOE) and modulus of rupture (MOR) are important wood properties for this species. In juvenile wood, which is formed within the first 10th–20th annual ring from the pith, low values of MOE and MOR are due to low values in wood density and high values of microfibril angle (MFA) of the S2 layer in tracheids (Zobel and van Buijitenen 1989; Moore and Cown 2017). The improvement of MOE and MOR, particularly in juvenile wood, enhances the future utilization of P. glehnii wood. In contrast, the effects of wood density and MFA on MOE and MOR in juvenile wood seem to differ from those in mature woods as reported for several coniferous wood species (Cown et al. 1999; Ishiguri et al. 2009; Tanabe et al. 2017). Therefore, the level of contribution of wood density and MFA to MOE and MOR should be considered for effective improvements of these traits.
A possible method to improve the mechanical properties of wood is genetic improvement using tree breeding programs. Wood properties are controlled not only by genetic factors but also by environmental factors (Zobel and Sprague 1998). When a wood property is more controlled by genetic factors than by environmental factors, the effect of genetic improvement programs is likely to be effective. In tree breeding for the improvement of wood quality in P. glehnii, variations in wood properties have been investigated mainly among plus-tree clones (Akutsu and Iizuka 1998; Iizuka et al. 1999, 2000). In contrast, information regarding among-family variations of wood properties in P. glehnii is limited (Iizuka et al. 2001; Tanabe et al. 2015). Lenz et al. (2011) pointed out that the optimal age of which selection maximizes genetic gain might vary because the contribution of genetic factors to wood properties varies with radial direction. Thus, among-family variation and within-tree radial variations of MOE and MOR and their related traits should be evaluated in P. glehnii to provide basic information regarding the age for selection in a tree breeding program.
In the present study, wood properties [MFA, air-dry density (AD), MOE, and MOR] were evaluated in nine open-pollinated families of P. glehnii grown in a progeny test site at Chitose, Hokkaido, Japan to clarify radial and among-family variations of wood properties and relationships between growth characteristics and wood properties. The possibility of exerting an early selection is also discussed.
2 Materials and methods
2.1 Materials
Samples were harvested from a progeny test site in Chitose, Hokkaido, Japan (42°47´N, 141°27´E). This progeny trial includes 15 families from five provenances. Open-pollinated seeds of P. glehnii were collected from 15 mother trees grown in five natural forests and used for preparing seedlings. Six-year-old seedlings were planted at the site in 1968 using a randomized complete block design with three replicates. Each plot comprised 150 trees from a family. The initial spacing between trees was 1.5 by 1.2 m (4200 tree ha–1). No pruning was applied until sampling. In December 2009, first thinning was conducted by removing a row of each plot. Of these thinned trees, intermediate or co-dominant trees were selected. Dominant, suppressed or abnormal trees with visible defects and trees grown in the edge of the plot were not selected as sample trees. Across three blocks, one to three trees per block were used while sample trees of Akan 104 and Honbetsu 111 were collected from single block. A total of 56 trees from nine open-pollinated families (approximately six trees per family) were used (Table 1).
| Table 1. Mean values and standard deviations of stem diameter and each wood property. | |||||||
| Family name | n | Stem diameter (cm) | ARW (mm) | MFA (degree) | AD (g cm–3) | MOE (GPa) | MOR (MPa) |
| Akan 101 | 9 | 20.5 ± 3.0 | 2.9 ± 0.4 | 9.5 ± 0.6 | 0.42 ± 0.03 | 8.57 ± 0.76 | 71.0 ± 4.8 |
| Akan 102 | 6 | 22.1 ± 3.6 | 3.0 ± 0.4 | 9.8 ± 0.6 | 0.43 ± 0.01 | 8.51 ± 0.39 | 72.0 ± 3.9 |
| Akan 104 | 4 | 20.3 ± 1.4 | 2.9 ± 0.2 | 10.9 ± 0.6 | 0.41 ± 0.03 | 7.51 ± 0.56 | 68.6 ± 4.1 |
| Asyoro 101 | 6 | 23.2 ± 5.0 | 3.1 ± 0.9 | 10.1 ± 0.6 | 0.40 ± 0.02 | 7.78 ± 0.64 | 66.1 ± 5.6 |
| Shirataki 102 | 7 | 19.8 ± 2.4 | 2.7 ± 0.4 | 10.1 ± 0.9 | 0.42 ± 0.02 | 8.44 ± 0.83 | 75.9 ± 6.0 |
| Honbetsu 106 | 7 | 17.2 ± 5.0 | 2.4 ± 0.6 | 9.0 ± 0.7 | 0.44 ± 0.02 | 8.85 ± 1.05 | 77.2 ± 9.6 |
| Honbetsu 107 | 6 | 21.0 ± 4.6 | 2.8 ± 0.6 | 9.7 ± 0.5 | 0.40 ± 0.02 | 7.67 ± 0.53 | 66.4 ± 4.2 |
| Honbetsu 111 | 4 | 19.7 ± 2.2 | 2.7 ± 0.3 | 9.0 ± 0.2 | 0.41 ± 0.02 | 8.23 ± 0.97 | 69.3 ± 6.7 |
| Rubeshibe 110 | 7 | 17.7 ± 3.6 | 2.5 ± 0.6 | 9.2 ± 0.8 | 0.41 ± 0.02 | 8.17 ± 0.58 | 71.0 ± 4.5 |
| Mean/Total | 56 | 20.2 ± 1.9 | 2.8 ± 0.2 | 9.7 ± 0.6 | 0.42 ± 0.01 | 8.19 ± 0.45 | 70.8 ± 3.8 |
| F-value | 1.684ns | 1.380ns | 4.588** | 2.150* | 2.246* | 2.775* | |
| ARW, annual ring width; MFA, microfibril angle of the S2 layer; AD, air-dry density; MOE, modulus of elasticity; MOR, modulus of rupture; **, significant difference (p < 0.01); *, significant difference (p < 0.05); ns, no significant difference among families. | |||||||
2.2 Measurements
Before felling, stem diameter at 1.3 m above the ground was measured for all sampled trees. Then, 3-cm-thick disks and 40-cm-length logs were collected from 1.3 to 1.8 m above the ground from each sampled tree.
The disk was cut into bark-to-bark strips for measuring the annual ring width (ARW). Image data on the transverse section of each bark-to-bark strip were captured by a scanner (MP-650, Canon, Tokyo, Japan) with a resolution of 300 dpi. ARW from the pith to the bark was measured on each annual ring in two directions on each bark-to-bark strip using ImageJ (Abràmoff et al. 2004). ARW in each tree was expressed by the mean value of ARW measured in the two directions.
Small wood blocks [approximately 5 (L) × 5 (R) × 5 (T) mm] were prepared from one side of each strip at every 5th annual ring (i.e., 5th, 10th, 15th, 20th, 25th, and 30th annual ring from the pith). MFA of the S2 layer in latewood tracheid was measured by the iodine method (Kobayashi 1952; Senft and Bendtsen 1985). Radial sections, 15-μm thick, were obtained from each block using a sliding microtome (REM-710, Yamato, Asaka, Japan). These sections were treated with Schulze’s solution (100 mL of 35% nitric acid containing 6 g of potassium chlorate) for 15 min, rinsed with distilled water, and dehydrated through a graded series of ethanol. Dehydrated sections were then immersed in a 2% iodine–potassium iodide solution, and a drop of 60% nitric acid was added to each section. Photomicrographs were taken using a digital camera (E-330, Olympus Corporation, Tokyo, Japan) attached to a light microscope (CX-41, Olympus Corporation, Tokyo, Japan). MFA was measured for each latewood tracheid using ImageJ on the digital photomicrographs; MFA was determined at each radial position by averaging the measurements of 30 latewood tracheids.
For the static bending test, three to four radial boards (3-cm in thick) were collected from three radial directions in 40-cm-length logs of each tree. These boards were air-dried in the laboratory without humidity control and planed into 1.5-cm thickness. Small clear specimens [240 (L) × 15 (R) × 15 (T) mm] were ripped from the planed boards. The annual ring number presented in the cross-section of each specimen was recorded and used to determine the radial variation of wood properties measured from small clear specimens according to the method described by Tanabe et al. (2014). Dimension and weight of each specimen were measured to determine AD of small clear specimens before the static bending test. Three point static bending test was conducted using a universal testing machine with a bending span of 210 mm (MSC-5/500-2, Tokyo Testing Machine, Tokyo, Japan). The load was applied at the radial face of center of the specimen at a speed of 2 mm min–1. MOE and MOR were determined using load-deflection diagrams. After the static bending test, small blocks were collected from each specimen to measure the moisture content. Moisture content values ranged from 7.5% to 9.6 % (8.6 ± 0.5%)
2.3 Data analysis
To evaluate the within-tree radial variation of wood properties (AD, MOE, and MOR), the methods described by Tanabe et al. (2014) were applied to data obtained from small clear specimens. Because of limited data obtained between the 16th–20th, 21st–25th, and 26th–30th annual ring, analysis of variance (ANOVA) among families was conducted to compare data obtained for the 1st–5th, 6th–10th, 11th–15th, and 16th–30th annual ring using an open source statistical software (R Core Team 2016). The coefficient of variation (CV) was calculated by dividing the standard deviation by the mean value of nine families at each position. Correlation coefficients (r) between ARW and wood properties were separately calculated for juvenile and mature woods. In this study, the boundary between juvenile and mature woods was assumed at the 15th annual ring from the pith according to a previous report on P. glehnii (Tanabe et al. 2015). Age–age correlation of each wood property was determined by calculating correlation coefficients between mean values from pith to bark and values at each radial position.
3 Results
Figs. 1 and 2 show the within-tree radial variation of wood properties. ARW gradually increased, reaching its maximum value at the 9th annual ring from the pith, after which it decreased until the 25th annual ring. Finally, ARW showed an almost constant value from the 25th to the 30th annual ring (Fig. 1). MFA showed the highest value at the 5th annual ring (ca. 18°), which gradually decreased and stabilized around 7° after the 15th annual ring (Fig. 1). AD decreased until the 11th–15th annual ring and increased thereafter (Fig. 2). The mean value of MOE across the nine families gradually increased to the 25th annual ring, stabilizing between the 21st–25th and 26th–30th annual ring. Family mean MOE values were 5.9 ± 0.5 GPa near the pith and around 10 GPa after the 25th annual ring from the pith (Fig. 2). MOR values were almost constant from the pith to the 15th annual ring (ca. 65 MPa). After this, MOR values increased after the 21st–30th annual ring (73–82 MPa, Fig. 2).
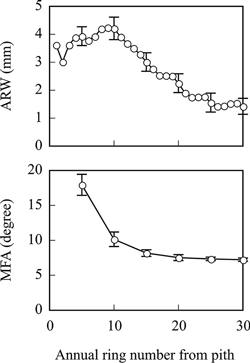
Fig. 1. Radial variation of the mean values of ARW and MFA in latewood tracheid of the nine families of Picea glehnii. Bars indicate standard deviation. ARW, annual ring width; MFA, microfibril angle of the S2 layer.
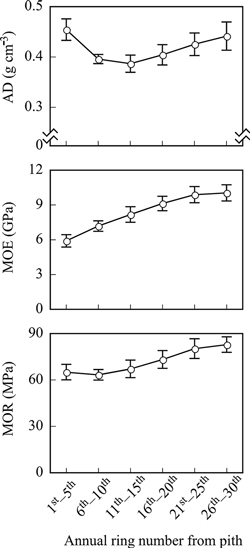
Fig. 2. Radial variations of mean values of AD, MOE, and MOR of the nine families of Picea glehnii. Bars indicate standard deviation. AD, air-dry density; MOE, modulus of elasticity; MOR, modulus of rupture.
Table 1 shows mean value from the pith to the 30th annual ring of each wood property and F-value obtained by ANOVA. The highest value of ARW was detected in Asyoro 101 (3.1 mm) and the lowest was Honbetsu 106. MFA in nine families ranged from 9.0° (Honbetsu 106 and Honbetsu 111) to 10.9° (Akan 104) and mean value was 9.7 ± 0.6°. The lowest and highest values of AD were 0.40 g cm–3 (Asyoro 101 and Honbetsu 107) and 0.44 g cm–3 (Honbetsu 106), respectively. Mean values of MOE and MOR ranged from 7.51 to 8.57 GPa and 66.1 to 77.2 MPa, respectively. Although F-value of stem diameter and ARW was not significant, significant differences among families were observed for MFA, AD MOE and MOR.
Table 2 shows F-values obtained by ANOVA and CV of each wood property traits at each radial position. Regarding among-family variations, the highest F-value for ARW was found at the 6th–10th annual ring from the pith. After the 11th annual ring, F-values were below 1.2, which indicated no significant difference among families. Statistically significant F-values in MFA were observed at all radial positions investigated. However, the highest F-value of MFA was obtained at the 6th–10th annual ring, followed by 16th–30th annual ring from the pith. F-values and CV for AD were almost constant at 1st–5th, 11th–15th, and 16th–30th annual ring from the pith, whereas those at the 6th–10th annual ring were smaller than those for other positions. Regarding MOE and MOR, significant differences were observed among families at the 1st–5th, 6th–10th, and 11th–15th annual ring from the pith, and the highest F-values were observed at the 11th–15th annual ring. In contrast, no significant differences among families were found in MOE and MOR after the 16th annual ring.
| Table 2. Age trends of F-values and coefficient of variation for each wood property. | ||||
| Annual ring number from the pith | ||||
| 1st–5th | 6th–10th | 11th–15th | 16th–30th | |
| ARW | 2.074ns (7.5) | 2.734* (9.2) | 1.208ns (9.2) | 1.131ns (15.5) |
| MFA | 3.937** (8.4) | 5.382** (10.2) | 2.536* (5.8) | 4.146** (3.8) |
| AD | 2.774* (4.7) | 0.611ns (2.3) | 2.483* (4.4) | 2.653* (4.7) |
| MOE | 2.667* (9.0) | 3.892** (6.3) | 4.652** (8.2) | 1.737ns (6.0) |
| MOR | 3.627** (7.7) | 2.729* (5.4) | 3.955** (8.4) | 1.702ns (6.6) |
| Values between parentheses indicate coefficients of variation calculated from nine mean values in each family at each position; ARW, annual ring width; MFA, microfibril angle of the S2 layer; AD, air-dry density; MOE, modulus of elasticity; MOR, modulus of rupture; **, significant difference (p < 0.01); *, significant difference (p < 0.05); ns, no significant difference among families. | ||||
Table 3 shows correlation coefficients between ARW and wood properties in juvenile and mature woods (the boundary between juvenile and mature woods was assumed to occur at the 15th annual ring from the pith). ARW in juvenile wood was not significantly correlated with other wood properties, whereas it was negatively correlated with AD, MOE, and MOR in mature wood.
| Table 3. Relationships between ARW and wood properties in juvenile and mature woods. | ||||
| MFA | AD | MOE | MOR | |
| Juvenile wood | 0.470ns | 0.101ns | –0.466ns | –0.553ns |
| Mature wood | 0.465ns | –0.778* | –0.723* | –0.768* |
| n = 9; ARW, annual ring width; MFA, microfibril angle of the S2 layer; AD, air-dry density; MOE, modulus of elasticity; MOR, modulus of rupture; **, significant correlation (p < 0.01); *, significant correlation (p < 0.05); ns, not significant. Juvenile wood: mean value of 1st–15th annual ring; mature wood: mean value of 16th–30th annual ring. | ||||
Positive significant correlation coefficients between mean values were obtained for all position except for AD and MOR at the 1st–5th annual ring and MOE at the 26th–30th annual ring AD (Table 4). The highest correlation coefficient between wood properties was obtained at the 6th–10th annual rings for MFA, MOE and MOR, whereas for AD, it was obtained at the 26th–30th annual ring from the pith.
| Table 4. Correlation coefficients between mean values from pith to bark and values at each age for each wood property. | ||||||
| 1st–5th | 6th–10th | 11th–15th | 16th–20th | 21st–25th | 26th–30th | |
| MFA | 0.923** | 0.972** | 0.931** | 0.866** | 0.780* | 0.903** |
| AD | 0.343ns | 0.869** | 0.779* | 0.771* | 0.779* | 0.919** |
| MOE | 0.758* | 0.961** | 0.896** | 0.791* | 0.821** | 0.611ns |
| MOR | 0.617ns | 0.897** | 0.772* | 0.841** | 0.863** | 0.871** |
| n = 9; MFA, microfibril angle of the S2 layer; AD, air-dry density; MOE, modulus of elasticity; MOR, modulus of rupture; **, significant correlation (p < 0.01); *, significant correlation (p < 0.05); ns, not significant. | ||||||
4 Discussions
4.1 Within-tree radial variation of wood properties
In the present study, the progeny test site was established by relatively dense spacing (4200 trees ha–1) compared to usual practice (2000–3000 trees ha–1) in Hokkaido district, Japan. Therefore, inter-tree competitions might occur in their early stage of growth. However, effect of narrower initial spacing on the results of ARW in the present study would be limited because suppressed trees were not sampled. A decrease of ARW after the 9th annual ring from the pith would be considered as crown of the site was closed at that time. Wider initial spacing or respacing before crown closure could delay the decrease of ARW, leading to increase in radial growth. Effects of stand density management on wood properties have been reported (Zovel and van Buijtenen 1989; Kuprevicius et al. 2013). Therefore, further research is needed for effect of wider spacing or respacing on wood properties as well as ARW in this species.
In general, the within-tree radial variation of MFA shows a decreasing trend from the pith until the 15th–20th annual ring and then stabilizes toward the bark in Picea species (Alteyrac et al. 2006a; Gräns et al. 2009; Lenz et al. 2010; Tanabe et al. 2015, 2017) and other conifers (Panshin and de Zeeuw 1980; Bendtsen and Senft 1986; Zobel and van Buijitenen 1989). This trend is also observed in P. glehnii. In a previous study, the clonal mean value of MFA in P. glehnii decreased from the pith (approximately 18°) until the 20th annual ring and became almost constant at approximately 8° (Tanabe et al. 2015). In the present study, similar values of MFA were observed, although the annual ring number at which the radial variation of MFA became stable was slightly different from that reported by Tanabe et al. (2015).
Other studies have reported that the within-tree radial variations of MFA can be used as an indicator to decide the boundary between juvenile and mature woods (Bendtsen and Senft 1986; Alteyrac et al. 2006b). In the present study, the boundary between juvenile and mature wood in nine families was considered to be at the 15th annual ring based on the radial variation of MFA (Fig. 1). Kawaguchi et al. (1986) have investigated the radial variation of tracheid length in 51-year-old P. glehnii trees and reported that the boundary between juvenile and mature woods range from the 15th to 21st annual ring from the pith. In plus-tree clones of P. glehnii, the juvenile–mature wood boundary was estimated to be at the 15th annual ring from the pith (Tanabe et al. 2015). Our results were similar to those reported previously, suggesting that the boundary between juvenile and mature woods in P. glehnii normally occurs around the 15th annual ring from the pith. However, some researchers have demonstrated that genetic/environmental differences as well as the method used to determine the boundary affect the transition age from juvenile to mature woods (Alteyrac et al. 2006b; Moore and Cown 2017). Thus, further research focused on measuring the genetic variation of transition age or juvenile wood ratio in this species is required.
The within-tree radial variation of wood density in Picea species was measured and generally categorized into the type II pattern of the Panshin and de Zeeuw’s classification (Panshin and de Zeeuw 1980): wood density decreases outward from the pith and increases to the bark (Kawaguchi et al. 1986; Kennedy 1995; Akutsu 1997; Alteyrac et al. 2006a; Gräns et al. 2009; Lenz et al. 2010; Tanabe et al. 2015). Our results are consistent with those of previous reports; therefore, radial variation of wood density in P. glehnii is regarded as the type II pattern in the classification of Panshin and de Zeeuw (1980).
In our study, both MOE and MOR values were in the range of those previously reported for P. glehnii (Kawaguchi et al. 1986; Akutsu 1997), P. glauca (Moench) Voss (Kuprevicious et al. 2013), and P. sitchensis (Bong.) Carrière (Mclean et al. 2016). The radial variation pattern of MOE observed was similar to that in other species, showing an increase in juvenile wood and becoming stable in mature wood (Zobel and van Buijtenen 1989). Compared with MOE, MOR showed a relatively small radial variation, particularly in juvenile wood. This result indicates that MOE is more variable than MOR in this species.
4.2 Radial variation of mechanical properties and effects of AD and MFA on them
Different effects of wood density and/or MFA on the mechanical properties of wood have been reported (Cown et al. 1999; Alteyrac et al. 2006a; Mclean et al. 2010, 2016). Some researchers have also found that the effects of these traits on the mechanical properties vary between juvenile and mature woods (Cown et al. 1999; Ishiguri et al. 2009; Tanabe et al. 2017). Cown et al. (1999) have reported in Pinus radiata D. Don that both wood density and MFA significantly affects MOE in juvenile wood, although wood density mostly contributed to MOE and MOR in mature wood. This tendency was also observed in P. jezoensis (Siebold et Zucc.) Carrière) (Tanabe et al. 2017). Our results were similar to those of these reports, although the correlation coefficient between MOE and AD in juvenile wood was not significant (r = 0.416 in 9 families). Therefore, in our results, different effects of wood density and/or MFA reflect radial variations of MOE and MOR.
Because of the strong negative relationship between MOE and MFA, the radial variation of MOE is the reverse of that of MFA (Alteyrac et al. 2006a). In the present study, although the radial variation of MOE showed the reverse pattern of that of MFA, the position of the annual ring at which MOE and MFA stabilized was different (Figs. 1 and 2). In contrast, the contribution of AD to MOE was larger in mature wood (r = 0.919), indicating that the initial increase in MOE might be due to a decrease in MFA until the 15th annual ring. With an increase in AD, an increase in MOE follows from the 16th to the 25th annual ring from the pith.
Because MOR is a mechanical property that relates to wood density, the radial variation of MOR follows that of wood density (Torquato et al. 2014). Kuprevicious et al. (2013) proposed that type II patterns of wood density in the classification of Panshin and de Zeeuw (1980) is caused by lower levels of the radial variation in MOR than in MOE in P. glauca. In addition, Ishiguri et al. (2009) also reported that MOR was almost constant from the pith to the bark in Cryptomeria japonica D. Don, although wood density near the pith showed a relatively higher value. In our study, the radial variation of AD in P. glehnii was also categorized into the type II pattern of the Panshin and de Zeeuw’s classification. Consistently, MOR values near the pith were not smaller than those from other outer rings and they did not stabilize outward from the pith. This may be due to the increase in AD at the corresponding positions. Our results suggest that MOE and MOR can be estimated using radial variations of MFA and/or AD at the given annual ring because these properties are correlated to MFA and/or AD.
4.3 Among-family variations
Zobel and van Buijtenen (1989) pointed out that wood properties are more genetically controlled than growth characteristics. The results of ANOVA for each property in P. glhenii used here revealed similar tendency: although stem diameter and ARW were not significantly differed among families, there were significant differences among families in MFA, AD, MOE and MOR (Table 1). This result emphasizes that improvement gains by conducting tree breeding programs in this species might be bigger in wood properties compared to growth characteristics. However, it has been reported that the magnitude of the effect of genetic factors on wood properties varies across radial direction (Hylen 1999; Iizuka et al. 2001; Kumar et al. 2006; Gräns et al. 2009; Lenz et al. 2010, 2011; Chen et al. 2014; Tanabe et al. 2014, 2015, 2017). Lenz et al. (2010) have reported three patterns of genetic effect on wood properties across radial direction in P. glauca: 1) heritability firstly increased and then became constant around the 10th annual ring, 2) heritability increased from the pith to the 16th annual ring, and 3) heritability showed almost constant value from the pith to the 16th annual ring. In contrast, it has also been reported that genetic effects might become unclear because of environmental effects such as crown closure, resulting in a lower heritability (or repeatability) in P. abies (L.) Karst. (Hylen 1999), P. glehnii (Iizuka et al. 2001), and P. radiata (Kumar et al. 2006).
F-values are used to measure the ratio of among-family variations to that of within-family variations; a higher F-value can be used as an indicator of a higher genetic control (Ide and Shiraishi 2012). In addition to F-values, CV reflects the degree of among-family variations in a trait (Lynch and Walsh 1998). Therefore, the radial position, where both F-value and CV in wood properties were estimated to be higher, would be expected to obtain significant genetic gain through genetic improvement programs. In the present study, similar to F-values, CVs at the 6th–10th or 11th–15th annual ring were generally higher than those after the 16th annual ring from the pith (Table 2). Remarkable decrease in F-value in ARW as increasing of annual rings might be due to increase in environmental effects, such as crown closure. However, although MOE and MOR also did not show significant differences among families at the 16th–30th annual ring, AD and MFA showed significant among-family variations in corresponding position. Therefore, environmental effects on degree of genetic control would be small in AD and MFA. When F-values were compared between mean values (Table 1) and each radial position (Table 2), F-values obtained from 6th–10th and 11th–15th annual ring from the pith were generally higher than those from mean values from pith to bark. Because larger amount of genetic variation indicates larger genetic gain, analyses for each radial position is favor to detect larger degree of among-family variation for selection, and useful for practical tree breeding in this species. Overall, among-family variations in P. glehnii are predominant in juvenile wood, indicating that the genetic improvement of wood properties is more effective at these positions. Therefore, to produce high quality timber, desirable juvenile wood quality should be one of the important criteria for selection of superior families in further tree breeding programs of P. glehnii.
4.4 Relationships between ARW and wood properties, and age–age correlations
Relationships between radial growth characteristics and wood properties, particularly wood density, in Picea species are generally negative (e.g., Zobel and van Buijtenen 1989; Rozenberg and Cahalan 1997). Interestingly, in our study, all investigated wood properties in juvenile wood were not significantly correlated to ARW (Table 3). The reason of this observation might be smaller variations of ARW in juvenile wood (less than 10% in CVs). Sampling strategy (no suppressed and dominant trees were used) in this study might be masked inter-tree competition during younger tree age, resulting in smaller variation of ARW in juvenile wood of this samples. On the other hand, there were families with both better radial growth and wood properties than mean values of nine families. This result suggests that selection of families with superior radial growth and wood properties would be possible in a tree breeding program in P. glehnii.
Age–age correlation coefficients of wood properties, particularly for wood density, were positively strong in Picea species (Rozenberg and Cahalan 1997; Iizuka et al. 1999, 2001; Gräns et al. 2009; Lenz et al. 2011; Chen et al. 2014; Tanabe et al. 2014;). Our results also indicate that an early evaluation of wood properties would be more effective using wood property data at the 6th–10th annual ring from the pith in P. glehnii (Table 4). In contrast, as described previously, F-values and CV of wood properties were also higher at the 6th–15th annual ring from the pith (Table 2), suggesting that progeny test at the 6th–15th annual ring from the pith is important in tree breeding for improved wood quality in P. glehnii. This suggestion is similar to that of Chen et al. (2014) who reported that early selection is more effective after the 10th annual ring because of lower heritability for earlier rings (e.g., 6th annual ring) in P. abies.
5 Conclusions
In this study, MFA, AD, MOE, and MOR were evaluated for nine open-pollinated families of P. glehnii grown in a progeny test site at Chitose, Hokkaido, Japan. All wood properties investigated showed different radial variations. The radial variation of MOR was relatively similar to that of AD, whereas the radial variation of MOE seemed to be related to MFA and AD, which may have been due to different effects of MFA and/or AD on MOE or MOR in juvenile and mature woods. Wood properties significantly differed among the nine families, particularly at the 6th–15th annual ring, except for ARW at the 11th–15th annual ring and AD at the 6th–10th annual ring, suggesting a larger contribution of genetic effect for these traits at these positions. In addition, CVs of these properties at the same positions were also high. Moreover, wood properties at the 6th–15th annual ring from the pith were positively correlated with overall mean values of these properties. Therefore, genetic improvements targeting wood properties for producing high quality timber in P. glehnii could be more effective by evaluating wood at the 6th–15th annual ring from the pith.
Acknowledgements
The authors would like to thank to Mr. Keita Sato for his great assistance for bending test.
References
Abràmoff M.D., Magalhães P.J., Ram S.J. (2004). Image processing with ImageJ. Biophotonics International 11: 36–42.
Akutsu H. (1997). Testing of wood qualities of Picea glehnii plantation (I): wood qualities of general planted trees. Journal of the Hokkaido Forest Products Research Institute 11: 1–5. [In Japanese with English summary].
Akutsu H., Iizuka K. (1998). Testing of wood qualities of Picea glehnii plantation (II): Wood qualities of plus-tree clones. Journal of the Hokkaido Forest Products Research Institute 12: 13–21. [In Japanese with English summary].
Alteyrac J., Cloutier A., Ung C.H., Zhang S.Y. (2006a). Mechanical properties in relation to selected wood characteristics of black spruce. Wood and Fiber Science 38: 229–237.
Alteyrac J., Cloutier A., Zhang S.Y. (2006b). Characterization of juvenile wood to mature wood transition age in black spruce (Picea mariana (Mill.) B.S.P.) at different stand densities and sampling heights. Wood Science and Technology 40(2): 124–138. https://doi.org/10.1007/s00226-005-0047-4.
Bendtsen B.A., Senft J. (1986). Mechanical and anatomical properties in individual growth rings of plantation-grown eastern cottonwood and loblolly pine. Wood and Fiber Science 18: 23–38.
Chen Z.Q., Gil M.R.G, Karlsson B., Lundqvist S.O., Olsson L., Wu H.X. (2014). Inheritance of growth and solid wood quality traits in a large Norway spruce population tested at two locations in southern Sweden. Tree Genetics & Genomes 10(5): 1291–1303. https://doi.org/10.1007/s11295-014-0761-x.
Cown D.J., Hebert J., Ball R. (1999). Modelling Pinus radiata lumber characteristics. Part 1: mechanical properties of small clears. New Zealand Journal of Forestry Science 29: 203–213.
Farjon A. (1990). Pinaceae. Koeltz Scientific Books, Königstein. 330 p.
Gräns D., Hannrup B., Isik F., Lundqvist S.O., McKeand S. (2009). Genetic variation and relationships to growth traits for microfibril angle, wood density and modulus of elasticity in a Picea abies clonal trial in southern Sweden. Scandinavian Journal of Forest Research 24: 494–503. https://doi.org/10.1080/02827580903280061.
Hylen G. (1999). Age trends in genetic parameters of wood density in young Norway spruce. Canadian Journal of Forest Research 29(1): 135–143. https://doi.org/10.1139/x98-170.
Ide Y., Shiraishi S. (2012). Forest tree breeding. Bunedo, Tokyo. 296 p. [In Japanese].
Iizuka K., Akutsu H., Itahana N. (1999). Clonal variation of wood quality in the grafted plus-trees of Picea glehnii. Journal of the Japanese Forestry Society 81: 325–329. [In Japanese with English summary].
Iizuka K., Hayashi E., Itahana N. (2000). Comparative analysis of growth and wood quality of Picea glehnii plus-tree-clones growing in various seed orchards. Journal of the Japan Forestry Society 82: 80–86. [In Japanese with English summary].
Iizuka K., Ubukata M., Sakamoto S. (2001). Geographic variations of growth and basic density in Picea glehnii. Journal of the Japanese Forestry Society 83: 53–57. [In Japanese with English summary].
Ishiguri F., Terazawa E., Sanpe H., Matsumoto K., Ishido M., Ohno H., Iizuka K., Yokota S., Yoshizawa N. (2009). Radial variation and difference between juvenile wood and mature wood in bending property of sugi (Cryptomeria japonica D. Don) originated from seedlings. Wood Industry 64: 20–25. [In Japanese with English summary].
Kawaguchi N., Takahashi M., Okubo I. (1986). The qualities of plantation-grown Akaezomatsu (I). Journal of the Hokkaido Forest Products Research Institute 416: 1–10. [In Japanese with English summary].
Kennedy R.W. (1995). Coniferous wood quality in the future: concerns and strategies. Wood Science and Technology 29(5): 321–338. https://doi.org/10.1007/BF00202581.
Kita K. (2008). Picea glehnii, P. jezoensis, P. abies. In: Forest Tree Breeding Association of Hokkaido (ed.). Forest tree breeding and forest genetic resources in Hokkaido. Forest Tree Breeding Association of Hokkaido, Ebetsu. p. 61–82. [In Janapese].
Kobayashi Y. (1952). A simple method for the preparation of sample for measurement of inclination of micelle in the wood cell wall. Journal Japan Forestry Society 34: 392–393. [In Japanese with English summary].
Kumar S., Dungey H.S., Matheson A.C. (2006). Genetic parameters and strategies for genetic improvement of stiffness in radiata pine. Silvae Genetica 55(1–6): 77–84. https://doi.org/10.1515/sg-2006-0012.
Kuprevicius A., Auty D., Achim A., Caspersen J.P. (2013). Quantifying the influence of live crown ratio on the mechanical properties of clear wood. Forestry 86(3): 361–369. https://doi.org/10.1093/forestry/cpt006.
Lenz P., Cloutier A., MacKey J., Beaulieu J. (2010). Genetic control of wood properties in Picea glauca – an analysis of trends with cambial age. Canadian Journal of Forest Research 40(4): 703–715. https://doi.org/10.1139/X10-014.
Lenz P., MacKay J., Rainville A., Cloutier A., Beaulieu J. (2011). The influence of cambial age on breeding for wood properties in Picea glauca. Tree Genetics and Genomes 7(3): 641–653. https://doi.org/10.1007/s11295-011-0364-8.
Lynch M., Walsh B. (1998). Genetics and analysis of quantitative traits. Sinauer, Sunderland. 980 p.
McLean J.P., Evans R., Moore J.R. (2010). Predicting the longitudinal modulus of elasticity of Sitka spruce from cellulose orientation and abundance. Holzforschung 64(4): 495–500. https://doi.org/10.1515/hf.2010.084.
McLean J.P., Moore J.R., Gardiner B.A., Lee S.J., Mochan S.J., Jarvis M.C. (2016). Variation of radial wood properties from genetically improved Sitka spruce growing in the UK. Forestry 89(2): 109–116. https://doi.org/10.1093/forestry/cpv035.
Moore J.R., Cown D.J. (2017). Corewood (juvenile wood) and its impact on wood utilization. Current Forestry Reports 3(2): 107–118. https://doi.org/10.1007/s40725-017-0055-2.
Ohba K., Katsuta M. (1991). Forest tree breeding. Buneido, Tokyo. 337 p. [In Japanese].
Panshin A.J., de Zeeuw C. (1980). Textbook of wood technology. Fourth edition. McGraw-Hill, New York. 722 p.
R Core Team (2016). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.
Rozenberg P., Cahalan C. (1997). Spruce and wood quality: genetic aspects (a review). Silvae Genetica 46: 270–279.
Senft J.F., Bendtsen B.A. (1985). Measuring microfibrilar angles using light microscopy. Wood and Fiber Science 17: 564–567.
Tanabe J., Tamura A., Hamanaka M., Ishiguri F., Takashima Y., Ohshima J., Iizuka K., Yokota S. (2014). Wood properties and their among-family variation in 10 open-pollinated families of Picea jezoensis. Journal of Wood Science 60(5): 297–304. https://doi.org/10.1007/s10086-014-1407-1.
Tanabe J., Tamura A., Ishiguri F., Takashima Y., Iizuka K., Yokota S. (2015). Inheritance of basic density and microfibril angle and their variations among full-sib families and their parental clones in Picea glehnii. Holzforschung 69(5): 581–586. https://doi.org/10.1515/hf-2014-0052.
Tanabe J., Ishiguri F., Tamura A., Ohshima J., Iizuka K., Yokota S. (2017). Radial and between-family variations of the microfibril angle and the relationships with bending properties in Picea jezoensis families. Scandinavian Journal of Forest Research 32(1): 39–44. https://doi.org/10.1080/02827581.2016.1186217.
Torquato L.P., Auty D., Hernandez R.E., Duchesne I., Porthier D., Achim A. (2014). Black spruce trees from fire-origin stands have higher wood mechanical properties than those from older, irregular stands. Canadian Journal of Forest Research 44(2): 118–127. https://doi.org/10.1139/cjfr-2013-0164.
Zobel B.J., Sprague J.R. (1998). Juvenile wood in forest trees. Springer-Verlag, Berlin, Heidelberg, New York. 300 p. https://doi.org/10.1007/978-3-642-72126-7.
Zobel B.J., van Buijtenen J.P. (1989). Wood variation: its causes and control. Springer-Verlag, Berlin, Heidelberg, New York. 363 p. https://doi.org/10.1007/978-3-642-74069-5.
Total of 39 references.

